Non-Parametric Frequency Warping
function [si] = specinterp(spec,indices); %SPECINTERP % [si] = specinterp(spec,indices); % % Returns spectrum sampled at indices (from 1). % Assumes a causal rectangular window was used. % The spec array should be the WHOLE spectrum, % not just 0 to half the sampling rate. % An "index" is a "bin number" + 1. % EXAMPLE: % N = 128; % x = sin(2*pi*0.1*[0:N-1]); % X = fft(x); % Xi = specinterp(X,[1:0.5:N]); % upsample by 2 % xi = ifft(x); % should now see 2x zero-padding N = length(spec); ibins = indices - 1; wki = ibins*2*pi/N; M = length(indices); si = zeros(1,M); wk = [0:N-1]*2*pi/N; for i=1:M index = indices(i); ri = round(index); if abs(index - ri) < 2*eps si(i) = spec(ri); else w = wki(i); % ideal interp kernel: wts = (1-exp(j*(wk-w)*N)) ./ (N*(1-exp(j*(wk-w)))); si(i) = sum(wts .* spec); end end |
Note that resampling a spectrum using the ideal interpolation kernel
requires
![]() operations, This computational burden can be
reduced in a number of ways:
operations, This computational burden can be
reduced in a number of ways:
- A window
 other than the rectangular window can be applied
to the data frame, so that
other than the rectangular window can be applied
to the data frame, so that
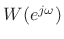 can be used as an interpolation
kernel in place of the aliased sinc function. If the window side lobes
are sufficiently small, they can be neglected. An example would be
can be used as an interpolation
kernel in place of the aliased sinc function. If the window side lobes
are sufficiently small, they can be neglected. An example would be
 set to a Hann window, with 50% overlap between frames, as
commonly used in the STFT.
set to a Hann window, with 50% overlap between frames, as
commonly used in the STFT.
- In pure frequency-warping applications, windows can be used for both analysis and reconstruction, as is done in apparently all perceptual audio coding methods such as MPEG [16,273]. For example, the square root of the Hann window can be applied to the analysis frame as well as the final overlap-add frame. This scheme has the advantage of tapering any discontinuities at the frame boundary more gracefully to zero, thus reducing the audibility of artifacts.
- Specially optimized narrow-support kernels can be designed by a number of methods [72,218]. If they are constrained to be nonnegative, their square root can be used twice like the Hann window in the previous point. Asymmetric factorizations are also possible when the kernel changes sign.
Next Section:
Fundamental Frequency Estimation
Previous Section:
Matlab for Unwrapping Spectral Phase



















