Free Books
   Free Books    Spectral Audio Signal Processing  

Power-of-Cosine Window Family

Definition:

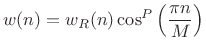$\displaystyle w(n)=w_R(n) \cos^P\left( \frac{ \pi n}{M} \right)$ (4.29)

where $ P$ is a nonnegative integer.

Properties:

  • The first 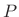$ P$ terms of the window's Taylor expansion, evaluated at the endpoints are identically 0 .
  • Roll-off rate 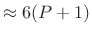$ \approx 6(P+1)$ dB/octave.

Special Cases:

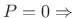  • $ P=0 \Rightarrow$ Rectangular window
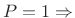  • $ P=1 \Rightarrow$ MLT sine window
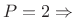  • $ P=2 \Rightarrow$ Hann window (``raised cosine'' = ``$ \cos^2$ '')
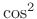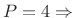  • $ P=4 \Rightarrow$ Alternative Blackman (maximized roll-off rate)

Thus, $ \cos^P$ windows parametrize $ L$ -term Blackman-Harris windows (for $ L=P/2+1$ ) which are configured to use all degrees-of-freedom to maximize roll-off rate.

Next Section:
Rectangular-Windowed Oboe Recording
Previous Section:
Frequency-Domain Implementation of the Blackman-Harris Family