Free Books
   Free Books    Spectral Audio Signal Processing  

Random Variable


Definition: A random variable $ x$ is defined as a real- or complex-valued function of some random event, and is fully characterized by its probability distribution.


Example: A random variable can be defined based on a coin toss by defining numerical values for heads and tails. For example, we may assign 0 to tails and 1 to heads. The probability distribution for this random variable is then

$\displaystyle \hat{p}(x) = \left\{\begin{array}{ll} \frac{1}{2}, & x = 0 \\ [5pt] \frac{1}{2}, & x = 1 \\ [5pt] 0, & \mbox{otherwise}. \\ \end{array} \right. \protect$ (C.4)


Example: A die can be used to generate integer-valued random variables between 1 and 6. Rolling the die provides an underlying random event. The probability distribution of a fair die is the discrete uniform distribution between 1 and 6. I.e.,

$\displaystyle \hat{p}(x) = \left\{\begin{array}{ll} \frac{1}{6}, & x = 1,2,\ldots,6 \\ [5pt] 0, & \mbox{otherwise}. \\ \end{array} \right.$ (C.5)


Example: A pair of dice can be used to generate integer-valued random variables between 2 and 12. Rolling the dice provides an underlying random event. The probability distribution of two fair dice is given by

$\displaystyle \hat{p}(x) = \left\{\begin{array}{ll} \frac{x-1}{36}, & x = 2,3,\ldots,7 \\ [5pt] \frac{13-x}{36}, & x = 7,8,\ldots,12 \\ [5pt] 0, & \mbox{otherwise}. \\ \end{array} \right.$ (C.6)

This may be called a discrete triangular distribution. It can be shown to be given by the convolution of the discrete uniform distribution for one die with itself. This is a general fact for sums of random variables (the distribution of the sum equals the convolution of the component distributions).


Example: Consider a random experiment in which a sewing needle is dropped onto the ground from a high altitude. For each such event, the angle of the needle with respect to north is measured. A reasonable model for the distribution of angles (neglecting the earth's magnetic field) is the continuous uniform distribution on $ [0,2\pi)$ , i.e., for any real numbers $ a$ and $ b$ in the interval $ [0,2\pi)$ , with $ a\leq b$ , the probability of the needle angle falling within that interval is

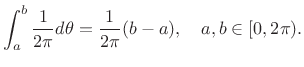$\displaystyle \int_a^b \frac{1}{2\pi}d\theta = \frac{1}{2\pi}(b-a), \quad a,b\in[0,2\pi).$ (C.7)

Note, however, that the probability of any single angle $ \theta$ is zero. This is our first example of a continuous probability distribution. Therefore, we cannot simply define the probability of outcome $ \theta$ for each $ \theta\in [0,2\pi)$ . Instead, we must define the probability density function (PDF):

$\displaystyle p(\theta) = \left\{\begin{array}{ll} \frac{1}{2\pi}, & 0\leq \theta < 2\pi \\ [5pt] 0, & \mbox{otherwise}. \\ \end{array} \right.$ (C.8)

To calculate a probability, the PDF must be integrated over one or more intervals. As follows from Lebesgue integration theory (``measure theory''), the probability of any countably infinite set of discrete points is zero when the PDF is finite. This is because such a set of points is a ``set of measure zero'' under integration. Note that we write $ \hat{p}(x)$ for discrete probability distributions and $ p(x)$ for PDFs. A discrete probability distribution such as that in (C.4) can be written as

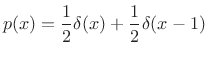$\displaystyle p(x) = \frac{1}{2}\delta(x) + \frac{1}{2}\delta(x-1)$ (C.9)

where $ \delta(x)$ denotes an impulse.C.1

Next Section:
Stochastic Process
Previous Section:
Independent Events