Independent Events
Two probabilistic events
and 
are said to be
independent if the probability of
and
occurring together equals the
product of the probabilities of
and
individually, i.e.,
 |
(C.2) |
where
denotes the probability of
and
occurring together.
Example:
Successive coin tosses are normally independent.
Therefore, the probability of getting heads twice in a row is
given by
 |
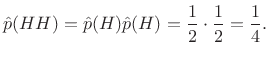(C.3) |
Next Section:
Random Variable
Previous Section:
Probability Distribution
