STFT of COLA Decomposition
To represent practical FFT implementations, it is preferable
to shift the ![]() frame back to the time origin:
frame back to the time origin:
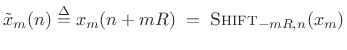 |
(9.20) |
This is summarized in Fig.8.11. Zero-based frames are needed because the leftmost input sample is assigned to time zero by FFT algorithms. In other words, a hopping FFT effectively redefines time zero on each hop. Thus, a practical STFT is a sequence of FFTs of the zero-based frames
Note that we may sample the DTFT of both ![]() and
and
![]() ,
because both are time-limited to
,
because both are time-limited to ![]() nonzero samples. The
minimum information-preserving sampling interval along the unit circle
in both cases is
nonzero samples. The
minimum information-preserving sampling interval along the unit circle
in both cases is
![]() . In practice, we often
oversample to some extent, using
. In practice, we often
oversample to some extent, using ![]() with
with ![]() instead. For
instead. For
![]() , we get
, we get
where
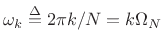 . For
. For
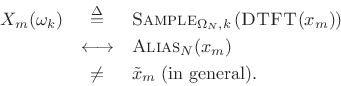
Since
![]() , their transforms are related by the
shift theorem:
, their transforms are related by the
shift theorem:

where ![]() denotes modulo
denotes modulo ![]() indexing (appropriate since the
DTFTs have been sampled at intervals of
indexing (appropriate since the
DTFTs have been sampled at intervals of
![]() ).
).
Next Section:
Acyclic Convolution
Previous Section:
COLA Examples








![\begin{psfrags}
% latex2html id marker 21934\psfrag{x}{$x$}\psfrag{Zero-centered 3rd frame x_3: M = 64, R = M/2}%
{\normalsize Zero-centered 3rd frame $x_3$: $M = 64$, $R = M/2$}\psfrag{x_3}{$x_3$} % doesn't work\psfrag{xtilde_3}{${\tilde x}_3$}\begin{figure}[htbp]
\includegraphics[width=\twidth]{eps/shiftwin}
\caption{Input signal $x$\ (top), third frame
$x_3$\ in its natural time location (middle), and the third frame
shifted to time 0, ${\tilde x}_3$\ (bottom).}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img1412.png)











