DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Acyclic Convolution

Getting back to acyclic convolution, we may write it as

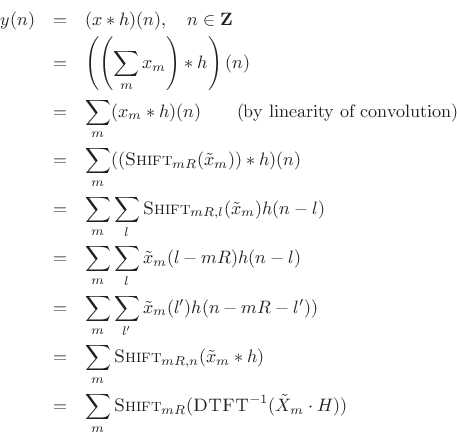
\begin{eqnarray*} y(n) &=& (x * h)(n), \quad n\in{\bf Z}\\ &=& \left ( \left( \sum_m x_m \right) * h \right)(n) \\ &=& \sum_m (x_m * h)(n) \qquad \hbox{(by linearity of convolution)}\\ &=& \sum_m (( \hbox{\sc Shift}_{mR}({\tilde x}_m)) * h)(n) \\ &=& \sum_m \sum_l \hbox{\sc Shift}_{mR,l}({\tilde x}_m)h(n-l) \\ &=& \sum_m \sum_l {\tilde x}_m(l-mR)h(n-l) \\ &=& \sum_m \sum_{l^{\prime}} {\tilde x}_m(l^{\prime})h(n-mR-l^{\prime})) \\ &=& \sum_m \hbox{\sc Shift}_{mR,n}( {\tilde x}_m * h) \\ &=& \sum_m \hbox{\sc Shift}_{mR} ( \hbox{\sc DTFT}^{-1}( {\tilde X}_m \cdot H) ) \\ \end{eqnarray*}

Since $ {\tilde x}_m$ is time limited to $ [0,\ldots,M-1]$ (or $ [-(M-1)/2,(M-1)/2]$ ), $ {\tilde X}_m$ can be sampled at intervals of $ \Omega_M = 2\pi/M$ without time aliasing. If $ h$ is time-limited to $ [0,L-1]$ , then $ {\tilde x}_m * h$ will be time limited to $ M+L-1$ . Therefore, we may sample $ {\tilde X}_m\cdot H$ at intervals of

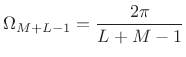$\displaystyle \Omega_{M+L-1} = \frac{2 \pi}{L+M-1}$ (9.22)

or less along the unit circle. This is the dual of the usual sampling theorem.

We conclude that practical FFT acyclic convolution may be carried out using an FFT of any length $ N$ satisfying

$\displaystyle N \ge M+L-1,$ (9.23)

where $ M$ is the frame size and $ L$ is the filter length. Our final expression for $ y(n)$ is

\begin{eqnarray*} y(n) &=& \sum_m \hbox{\sc Shift}_{mR,n} \left[\frac{1}{N} \sum_{k=0}^{N-1} {\tilde H}(\omega_k) {\tilde X}_m(\omega_k) e^{j\omega_k n T}\right]\\ &=& \sum_m \hbox{\sc Shift}_{mR,n}\left\{ \hbox{\sc IFFT}_N[\hbox{\sc FFT}_N({\tilde x}_m)\cdot \hbox{\sc FFT}_N(h)]\right\}, \end{eqnarray*}

where $ {\tilde X}_m$ is the length $ N$ DFT of the zero-padded $ m^{\mbox{th}}$ frame $ {\tilde x}_m$ , and $ {\tilde H}$ is the length $ N$ DFT of $ h$ , also zero-padded out to length $ N$ , with $ N\geq L+M-1$ .

Note that the terms in the outer sum overlap when $ R<M$ even if $ H(\omega_k)\equiv1$ . In general, an LTI filtering by $ H$ increases the amount of overlap among the frames.

This completes our derivation of FFT convolution between an indefinitely long signal $ x(n)$ and a reasonably short FIR filter $ h(n)$ (short enough that its zero-padded DFT can be practically computed using one FFT).

The fast-convolution processor we have derived is a special case of the Overlap-Add (OLA) method for short-time Fourier analysis, modification, and resynthesis. See [7,9] for more details.

Next Section:
Example of Overlap-Add Convolution
Previous Section:
STFT of COLA Decomposition