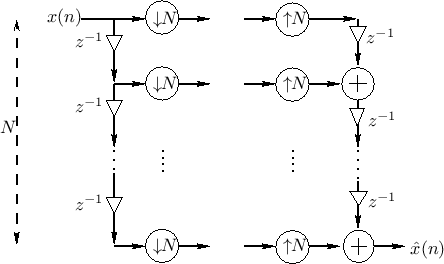
Simple Examples of Perfect Reconstruction
If we can arrange to have
| (12.55) |
then the filter bank will reduce to the simple system shown in Fig.11.23.
Thus, when ![]() and
and
![]() ,
we have a simple parallelizer/serializer,
which is perfect-reconstruction by inspection: Referring to
Fig.11.23, think of the input samples
,
we have a simple parallelizer/serializer,
which is perfect-reconstruction by inspection: Referring to
Fig.11.23, think of the input samples ![]() as ``filling'' a
length
as ``filling'' a
length ![]() delay line over
delay line over ![]() sample clocks. At time 0
, the
downsamplers and upsamplers ``fire'', transferring
sample clocks. At time 0
, the
downsamplers and upsamplers ``fire'', transferring ![]() (and
(and ![]() zeros) from the delay line to the output delay chain, summing with
zeros. Over the next
zeros) from the delay line to the output delay chain, summing with
zeros. Over the next ![]() clocks,
clocks, ![]() makes its way toward the
output, and zeros fill in behind it in the output delay chain.
Simultaneously, the input buffer is being filled with samples of
makes its way toward the
output, and zeros fill in behind it in the output delay chain.
Simultaneously, the input buffer is being filled with samples of
![]() . At time
. At time ![]() ,
, ![]() makes it to the output. At time
makes it to the output. At time ![]() ,
the downsamplers ``fire'' again, transferring a length
,
the downsamplers ``fire'' again, transferring a length ![]() ``buffer''
[
``buffer''
[![]() :
:![]() ] to the upsamplers. On the same clock pulse, the
upsamplers also ``fire'', transferring
] to the upsamplers. On the same clock pulse, the
upsamplers also ``fire'', transferring ![]() samples to the output delay
chain. The bottom-most sample [
samples to the output delay
chain. The bottom-most sample [
![]() ] goes out immediately
at time
] goes out immediately
at time ![]() . Over the next
. Over the next ![]() sample clocks, the length
sample clocks, the length ![]() output buffer will be ``drained'' and refilled by zeros.
Simultaneously, the input buffer will be replaced by new samples of
output buffer will be ``drained'' and refilled by zeros.
Simultaneously, the input buffer will be replaced by new samples of
![]() . At time
. At time ![]() , the downsamplers and upsamplers ``fire'', and
the process goes on, repeating with period
, the downsamplers and upsamplers ``fire'', and
the process goes on, repeating with period ![]() . The output of the
. The output of the
![]() -way parallelizer/serializer is therefore
-way parallelizer/serializer is therefore
| (12.56) |
and we have perfect reconstruction.
Next Section:
Sliding Polyphase Filter Bank
Previous Section:
Orthogonal Two-Channel Filter Banks