DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

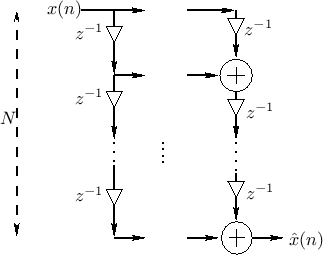
Sliding Polyphase Filter Bank

Figure: Simplified filter bank when $ R(z)$ inverts $ E(z)$ and there are no downsamplers or upsamplers ($ R=1$ ).
\includegraphics{eps/polyNchanIR1}

When $ R=1$ , there is no downsampling or upsampling, and the system further reduces to the case shown in Fig.11.24. Working backward along the output delay chain, the output sum can be written as

\begin{eqnarray*} \hat{X}(z) &=& \left[z^{-0}z^{-(N-1)} + z^{-1}z^{-(N-2)} + z^{-2}z^{-(N-3)} + \cdots \right.\\ & & \left. + z^{-(N-2)}z^{-1} + z^{-(N-1)}z^{-0} \right] X(z)\\ &=& N z^{-(N-1)} X(z). \end{eqnarray*}

Thus, when $ R=1$ , the output is

$\displaystyle {\hat x}(n) \eqsp N x(n-N+1)$ (12.57)

and we again have perfect reconstruction.

Next Section:
Hopping Polyphase Filter Bank
Previous Section:
Simple Examples of Perfect Reconstruction