DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Sines+Noise Summary

To summarize, sines+noise modeling is carried out by a procedure such as the following:

  • Compute a sinusoidal model by tracking peaks across STFT frames, producing a set of amplitude envelopes 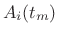$ A_i(t_m)$ and frequency envelopes 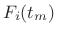$ F_i(t_m)$ , where $ m$ is the frame number and $ i$ is the spectral-peak number.

  • Also record phase 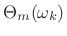$ \Theta_m(\omega_k)$ for frames containing a transient.

  • Subtract modeled peaks from each STFT spectrum to form a residual spectrum.

  • Fit a smooth spectral envelope $ H_m(\omega_k)$ to each residual spectrum.

  • Convert envelopes to reduced form, e.g., piecewise linear segments with nonuniformly distributed breakpoints (optimized to be maximally sparse without introducing audible distortion).

  • Resynthesize audio (along with any desired transformations) from the amplitude, frequency, and noise-floor-filter envelopes.

  • Alter frequency trajectories slightly to hit the desired phase for transient frames (as described below equation Eq.$ \,$ (10.19)).

Because the signal model consists entirely of envelopes (neglecting the phase data for transient frames), the signal model is easily time scaled, as discussed further in §10.5 below.

For more information on sines+noise signal modeling, see, e.g., [146,10,223,248,246,149,271,248,271]. A discussion from an historical perspective appears in §G.11.4.

Next Section:
Sines+Noise+Transients Time-Frequency Maps
Previous Section:
S+N Synthesis