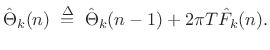Following Spectral Peaks
In the analysis phase, sinusoidal peaks are measured over time in a sequence of FFTs, and these peaks are grouped into ``tracks'' across time. A detailed discussion of various options for this can be found in [246,174,271,84,248,223,10,146], and a particular case is detailed in Appendix H.
The end result of the analysis pass is a collection of amplitude and
frequency envelopes for each spectral peak versus time. If the time
advance from one FFT to the next is fixed (5ms is a typical choice for
speech analysis), then we obtain uniformly sampled amplitude and
frequency trajectories as the result of the analysis. The sampling
rate of these amplitude and frequency envelopes is equal to
the frame rate of the analysis. (If the time advance between
FFTs is
ms, then the frame rate is defined as
Hz.) For resynthesis using inverse FFTs, these data may be
used unmodified. For resynthesis using a bank of sinusoidal
oscillators, on the other hand, we must somehow
interpolate the envelopes to create envelopes at the signal
sampling rate (typically 
kHz or higher).
It is typical in computer music to linearly interpolate the
amplitude and frequency trajectories from one frame to the next
[271].11.10 Let's call the piecewise-linear upsampled envelopes
and
, defined now for all 
at the normal signal
sampling rate. For steady-state tonal sounds, the phase may be
discarded at this stage and redefined as the integral of the
instantaneous frequency when needed:
When phase must be matched in a given frame, such as when it is known to contain a transient event, the frequency can instead move quadratically across the frame to provide cubic phase interpolation [174], or a second linear breakpoint can be introduced somewhere in the frame for the frequency trajectory (in which case the area under the triangle formed by the second breakpoint equals the added phase at the end of the segment).
Next Section:
Sinusoidal Peak Finding
Previous Section:
Linear Prediction in Matlab and Octave
