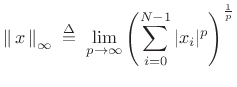Special Cases

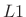norm

$\displaystyle \left\Vert\,x\,\right\Vert _1 \isdefs \sum_{i=0}^{N-1} \vert x_i\vert$ (5.28)
- Sum of the absolute values of the elements
- ``City block'' distance
norm

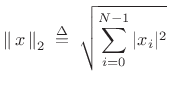
$\displaystyle \left\Vert\,x\,\right\Vert _2 \isdefs \sqrt{ \sum_{i=0}^{N-1} \vert x_i\vert^2 }$ (5.29)
- ``Euclidean'' distance
- Minimized by ``Least Squares'' techniques
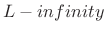norm

$\displaystyle \left\Vert\,x\,\right\Vert _\infty \isdefs \lim_{p\to\infty} \left( \sum_{i=0}^{N-1} \vert x_i\vert^p \right)^\frac{1}{p} \protect$ (5.30)

In the limit as 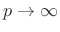$p \rightarrow \infty$ , the 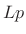norm of is dominated by the maximum element of . Optimal Chebyshev filters minimize this norm of the frequency-response error.