Filter Design using Lp Norms
Formulated as an 
norm minimization, the FIR filter design problem
can be stated as follows:
![$\displaystyle \min_h \left\Vert W(\omega_k)\left[H(\omega_k) - D(\omega_k)\right]\right\Vert _p$](http://www.dsprelated.com/josimages_new/sasp2/img831.png){kind=small} |
(5.31) |
where
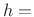FIR filter coefficients
-
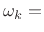suitable discrete set of frequencies
-
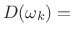desired (complex) frequency response
-
obtained frequency response (typically fft(h))
-
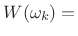(optional) error weighting function
norms
is that the error norm is typically a convex function of the
filter coefficients, rendering it amenable to a wide variety of
convex-optimization algorithms [22]. The following sections
look at some specific cases.
Next Section:
Geometric Interpretation of Least Squares
Previous Section:
Special Cases
