DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Summary of LP Spectral Envelopes

In summary, the spectral envelope of the $ m$ th spectral frame, computed by linear prediction, is given by

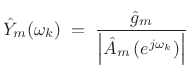$\displaystyle {\hat Y}_m(\omega_k) \eqsp \frac{{\hat g}_m}{\left\vert{\hat A}_m\left(e^{j\omega_k }\right)\right\vert}$ (11.13)

where $ {\hat A}_m$ is computed from the solution of the Toeplitz normal equations, and $ {\hat g}_m = \vert\vert\,{\hat E}_m\,\vert\vert _2$ is the estimated rms level of the prediction error in the $ m$ th frame.

The stable, all-pole filter

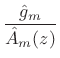$\displaystyle \frac{{\hat g}_m}{{\hat A}_m(z)}$ (11.14)

can be driven by unit-variance white noise to produce a filtered-white-noise signal having spectral envelope $ {\hat g}_m/\vert{\hat A}_m(e^{j\omega_k })\vert$ . We may regard $ {\hat g}_m/{\hat A}_m(e^{j\omega_k })$ (no absolute value) as the frequency response of the filter in a source-filter decomposition of the signal $ y_m(n)$ , where the source is white noise.

It bears repeating that $ \log A(e^{j\omega_k })$ is zero mean when $ A(z)$ is monic and minimum phase (all zeros inside the unit circle). This means, for example, that $ \log {\hat g}_m$ can be simply estimated as the mean of the log spectral magnitude $ \log \vert Y_m(e^{j\omega_k })\vert$ .

For best results, the frequency axis ``seen'' by linear prediction should be warped to an auditory frequency scale, as discussed in Appendix E [123]. This has the effect of increasing the accuracy of low-frequency peaks in the extracted spectral envelope, in accordance with the nonuniform frequency resolution of the inner ear.

Next Section:
Signal Synthesis
Previous Section:
Linear Prediction Order Selection