DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Synthesis (Step 7)

The analysis portion of PARSHL returns a set of amplitudes $ \hat{A}^m$ , frequencies $ \hat{\omega}^m$ , and phases $ \hat{\theta}^m$ , for each frame index $ m$ , with a ``triad'' ( $ \hat{A}_r^m, \hat{\omega}_r^m, \hat{\theta}_r^m$ ) for each track $ r$ . From this analysis data the program has the option of generating a synthetic sound.

The synthesis is done one frame at a time. The frame at hop $ m$ , specifies the synthesis buffer

$\displaystyle s^m(n) = \sum_{r=1}^{R^m} \hat{A}_{r}^m \cos [n\hat{\omega}_{r}^m + \hat{\theta}_{r}^m]$ (H.9)

where $ R^m$ is the number of tracks present at frame $ m$ ; $ m=0,1,2, \ldots ,S-1$ ; and $ S$ is the length of the synthesis buffer (without any time scaling $ S=R$ , the analysis hop size). To avoid ``clicks'' at the frame boundaries, the parameters ( $ \hat{A}_r^m, \hat{\omega}_r^m, \hat{\theta}_r^m$ ) are smoothly interpolated from frame to frame.

The parameter interpolation across time used in PARSHL is the same as that used by McAulay and Quatieri [174]. Let ( $ \hat{A}_r^{(m-1)}, \hat{\omega}_r^{(m-1)}, \hat{\theta}_r^{(m-1)}$ ) and ( $ \hat{A}_r^m, \hat{\omega}_r^m, \hat{\theta}_r^m$ ) denote the sets of parameters at frames $ m-1$ and $ m$ for the $ r$ th frequency track. They are taken to represent the state of the signal at time 0 (the left endpoint) of the frame.

The instantaneous amplitude $ \hat{A}(n)$ is easily obtained by linear interpolation,

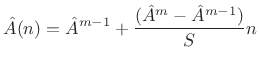$\displaystyle \hat{A}(n)= \hat{A}^{m-1} + {{(\hat{A}^m - \hat{A}^{m-1})} \over S} n$ (H.10)

where $ n= 0, 1, \ldots, S-1$ is the time sample into the $ m$ th frame.

Frequency and phase values are tied together (frequency is the phase derivative), and they both control the instantaneous phase $ \hat{\theta}(n)$ . Given that four variables are affecting the instantaneous phase: $ \hat{\omega}^{(m-1)}, \hat{\theta}^{(m-1)}, \hat{\omega}^m$ , and $ \hat{\theta}^m$ , we need at least three degrees of freedom for its control, while linear interpolation only gives one. Therefore, we need at least a cubic polynomial as interpolation function, of the form

$\displaystyle \hat{\theta}(n) = \zeta + \gamma n + \alpha n^2 + \beta n^3.$ (H.11)

We will not go into the details of solving this equation since McAulay and Quatieri [174] go through every step. We will simply state the result:

$\displaystyle \hat{\theta}(n) = \hat{\theta}^{(m-1)} + \hat{\omega}^{(m-1)} n + \alpha n^2 + \beta n^3$ (H.12)

where $ \alpha $ and $ \beta $ can be calculated using the end conditions at the frame boundaries,
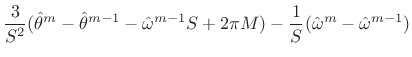$\displaystyle \alpha$ $\displaystyle =$ $\displaystyle {3\over {S^2}} {(\hat{\theta}^m - \hat{\theta}^{m-1} - \hat{\omega} ^{m-1} S + 2\pi M) - {1\over S} (\hat{\omega}^m - \hat{\omega}^{m-1})}$ (H.13)
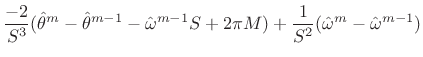$\displaystyle \beta$ $\displaystyle =$ $\displaystyle {-2\over {S^3}} {(\hat{\theta}^m - \hat{\theta}^{m-1} - \hat{\omega} ^{m-1} S + 2\pi M) + {1\over {S^2}} (\hat{\omega}^m - \hat{\omega}^{m-1})}$ (H.14)

This will give a set of interpolating functions depending on the value of $ M$ , among which we have to select the ``maximally smooth'' one. This can be done by choosing $ M$ to be the integer closest to $ x$ , where $ x$ is [174, Eq.(36)]

$\displaystyle x= {1\over 2\pi} \left[(\hat{\theta}^{m-1} + \hat{\omega}^{m-1} S - \hat{\theta}^m) + (\hat{\omega}^m - \hat{\omega}^{m+1}) {S\over 2}\right]$ (H.15)

and finally, the synthesis equation turns into

$\displaystyle s^m(n) = \sum_{r=1}^{R^m} \hat{A}_{r}^m(n) \cos [\hat{\theta}_{r}^m(n)]$ (H.16)

which smoothly goes from frame to frame and where each sinusoid accounts for both the rapid phase changes (frequency) and the slowly varying phase changes.

Figure H.5 shows the result of the analysis/synthesis process using phase information and applied to a piano tone.

Figure H.5: (a) Original piano tone, (b) synthesis with phase information, (c) synthesis without phase information.
\includegraphics[width=\twidth]{eps/fig8}

Next Section:
Magnitude-only Analysis/Synthesis
Previous Section:
Parameter Modifications (Step 6)