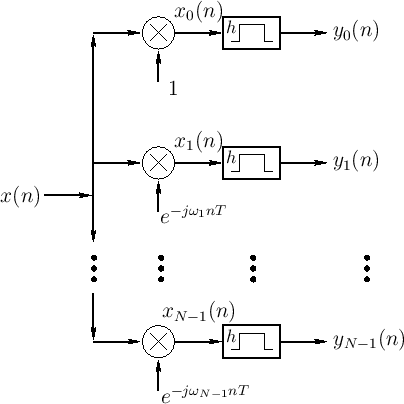
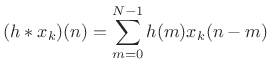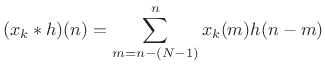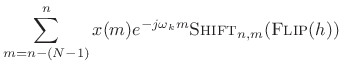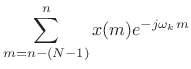System Diagram of the Running-Sum Filter Bank

**Figure 9.15:** DFT Filter Bank.
$\includegraphics{eps/BPFB}$

Figure 9.15 shows the system diagram of the complete -channel filter bank constructed using length FIR running-sum lowpass filters. The th channel computes:

$\displaystyle y_k(n)$	$\displaystyle =$	$\displaystyle (h\ast x_k)(n) = \sum_{m=0}^{N-1}h(m)x_k(n-m)$
	$\displaystyle =$	$\displaystyle (x_k\ast h)(n) = \sum_{m=n-(N-1)}^{n}x_k(m)h(n-m)$
	$\displaystyle =$	$\displaystyle \sum_{m=n-(N-1)}^{n}x(m)e^{-j\omega_k m }\hbox{\sc Shift}_{n,m}(\hbox{\sc Flip}(h))$
	$\displaystyle =$	$\displaystyle \sum_{m=n-(N-1)}^{n}x(m)e^{-j\omega_k m } \protect$	(10.12)