Type II Polyphase Decomposition
The polyphase decomposition of 
into 
channels in
(11.11) may be termed a ``type I'' polyphase decomposition. In
the ``type II'', or reverse polyphase decomposition, the powers
of 
progress in the opposite direction:
 |
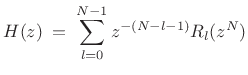(12.14) |
We will see that we need type I for analysis filter banks and type II for synthesis filter banks in a general ``perfect reconstruction filter bank'' analysis/synthesis system.
Next Section:
Filtering and Downsampling, Revisited
Previous Section:
N-Channel Polyphase Decomposition
