N-Channel Polyphase Decomposition
For the general case of arbitrary ![]() , the basic idea is to decompose
, the basic idea is to decompose
![]() into its periodically interleaved subsequences, as indicated
schematically in Fig.11.9. The polyphase decomposition into
into its periodically interleaved subsequences, as indicated
schematically in Fig.11.9. The polyphase decomposition into
![]() channels is given by
channels is given by
where the subphase filters are defined by
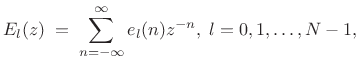 |
(12.12) |
with
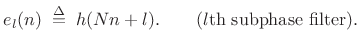 |
(12.13) |
The signal
Next Section:
Type II Polyphase Decomposition
Previous Section:
Two-Channel Case








![\includegraphics[scale=0.8]{eps/polytime}](http://www.dsprelated.com/josimages_new/sasp2/img1965.png)
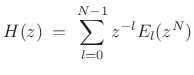
![\begin{psfrags}
% latex2html id marker 29755\psfrag{M}{{\normalsize $N$}}\psfrag{ztl}{{\Large $z^l$}}\psfrag{h[n]}{{\Large $h(n)$}}\psfrag{eln}{{\Large $e_l(n)$}}\begin{figure}[htbp]
\includegraphics[width=0.5\twidth]{eps/polypick}
\caption{Advance by $l$\ samples followed by a downsampling by the factor $N$.}
\end{figure}
\end{psfrags}](http://www.dsprelated.com/josimages_new/sasp2/img1970.png)











