DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Upsampling (Stretch) Operator

Figure: Upsampling by a factor of $ N$ : $ y \isdeftext \hbox{\sc Stretch}_N(x)$ .
\includegraphics{eps/upsample}

Figure 11.1 shows the graphical symbol for a digital upsampler by the factor $ N$ . To upsample by the integer factor $ N$ , we simply insert $ N-1$ zeros between $ x(n)$ and $ x(n+1)$ for all $ n$ . In other words, the upsampler implements the stretch operator defined in §2.3.9:

\begin{eqnarray*} y(n) &=& \hbox{\sc Stretch}_{N,n}(x)\\ &\isdef & \left\{\begin{array}{ll} x(n/N), & \frac{n}{N}\in{\bf Z} \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right. \end{eqnarray*}

In the frequency domain, we have, by the stretch (repeat) theorem for DTFTs:

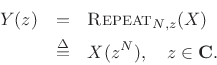
\begin{eqnarray*} Y(z) &=& \hbox{\sc Repeat}_{N,z}(X)\\ &\isdef & X(z^N), \quad z\in{\bf C}. \end{eqnarray*}

Plugging in $ z=e^{j\omega}$ , we see that the spectrum on $ [-\pi,\pi)$ contracts by the factor $ N$ , and $ N$ images appear around the unit circle. For $ N=2$ , this is depicted in Fig.11.2.

Figure: Illustration of $ \hbox {\sc Repeat}_2$ in the frequency domain.
\includegraphics[width=0.8\twidth]{eps/upsampspec}

Next Section:
Downsampling (Decimation) Operator
Previous Section:
Optimal Band Filters