Downsampling (Decimation) Operator

Free Books Spectral Audio Signal Processing

**Figure:** Downsampling by .
$\includegraphics{eps/downsample}$

Figure 11.3 shows the symbol for downsampling by the factor . The downsampler selects every th sample and discards the rest:

$\begin{eqnarray*} y(n) &=& \hbox{\sc Downsample}_{N,n}(x)\\ &\isdef & x(Nn), \quad n\in{\bf Z} \end{eqnarray*}$

In the frequency domain, we have

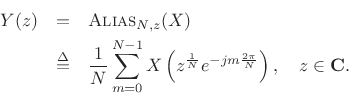
$\begin{eqnarray*} Y(z) &=& \hbox{\sc Alias}_{N,z}(X)\\ &\isdef & \frac{1}{N} \sum_{m=0}^{N-1} X\left(z^\frac{1}{N}e^{-jm\frac{2\pi}{N}} \right), \quad z\in{\bf C}. \end{eqnarray*}$

Thus, the frequency axis is expanded by the factor , wrapping times around the unit circle, adding to itself times. For , two partial spectra are summed, as indicated in Fig.11.4.

**Figure:** Illustration of **$\hbox {\sc Alias}_2$** in the frequency domain.
$\includegraphics[width=0.8\twidth]{eps/dnsampspec}$

Using the common twiddle factor notation

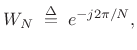$\displaystyle W_N \isdefs e^{-j2\pi/N},$

(12.1)

the aliasing expression can be written as

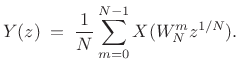
$\displaystyle Y(z) \eqsp \frac{1}{N} \sum_{m=0}^{N-1} X(W_N^m z^{1/N}).$

Example: Downsampling by 2

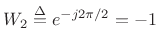For , downsampling by 2 can be expressed as , so that (since $W_2\isdef e^{-j2\pi/2}=-1$ )

$\begin{eqnarray*} Y(z) &=& \frac{1}{2}\left[X\left(W^0_2 z^{1/2}\right) + X\left(W^1_2 z^{1/2}\right)\right] \\ [5pt] &=& \frac{1}{2}\left[X\left(e^{-j2\pi 0/2} z^{1/2}\right) + X\left(e^{-j2\pi 1/2}z^{1/2}\right)\right] \\ [5pt] &=& \frac{1}{2}\left[X\left(z^{1/2}\right) + X\left(-z^{1/2}\right)\right] \\ [5pt] &=& \frac{1}{2}\left[\hbox{\sc Stretch}_2(X) + \hbox{\sc Stretch}_2\left(\hbox{\sc Shift}_\pi(X)\right)\right]. \end{eqnarray*}$