Summary of ROC Rules

This is a very short guide on how to find all possible outcomes of a system where Region of Convergence (ROC) and the original signal is not known.

Summary of ROC Rules

1. For a causal system the ROC extends outwards.
2. For a non-causal system the ROC extends inwards.
3. For a two-sided system, the ROC can extend inwards or outwards from every pole. 
4. The ROC cannot contain any poles
5. The system is stable if the unity circle is included in the ROC

One Pole System Example

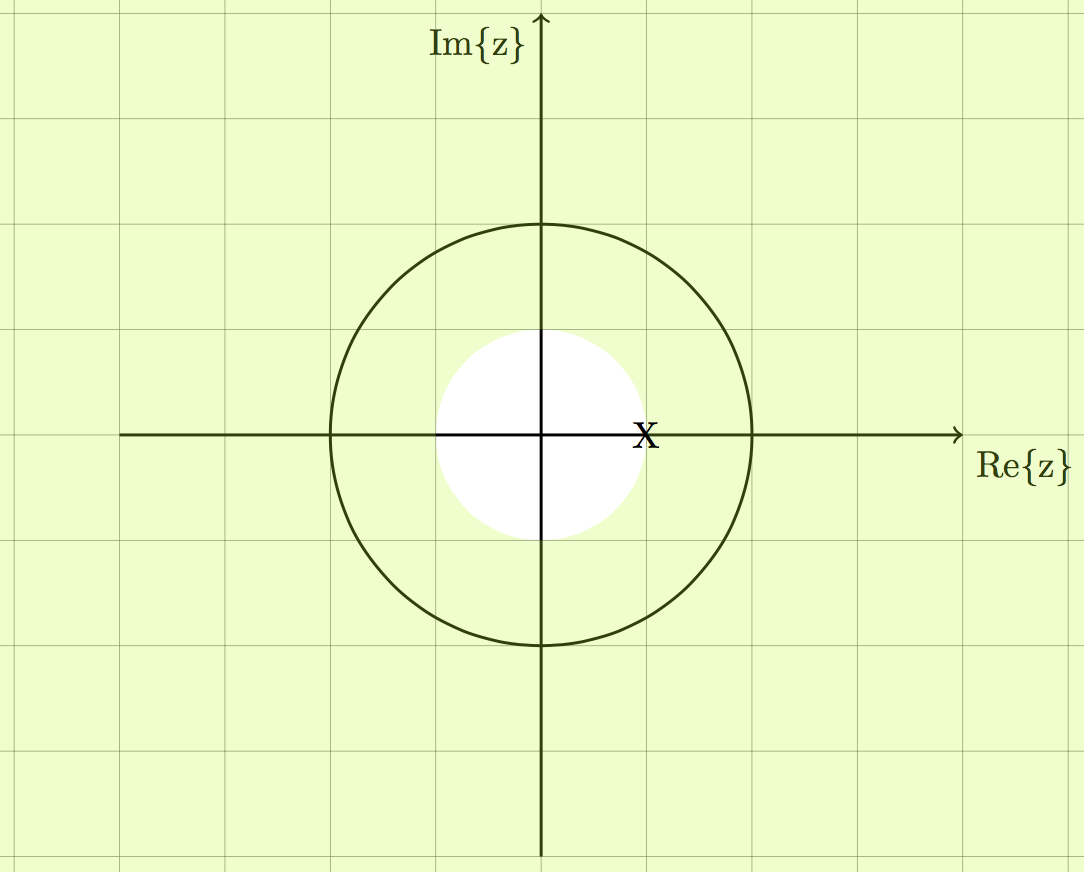
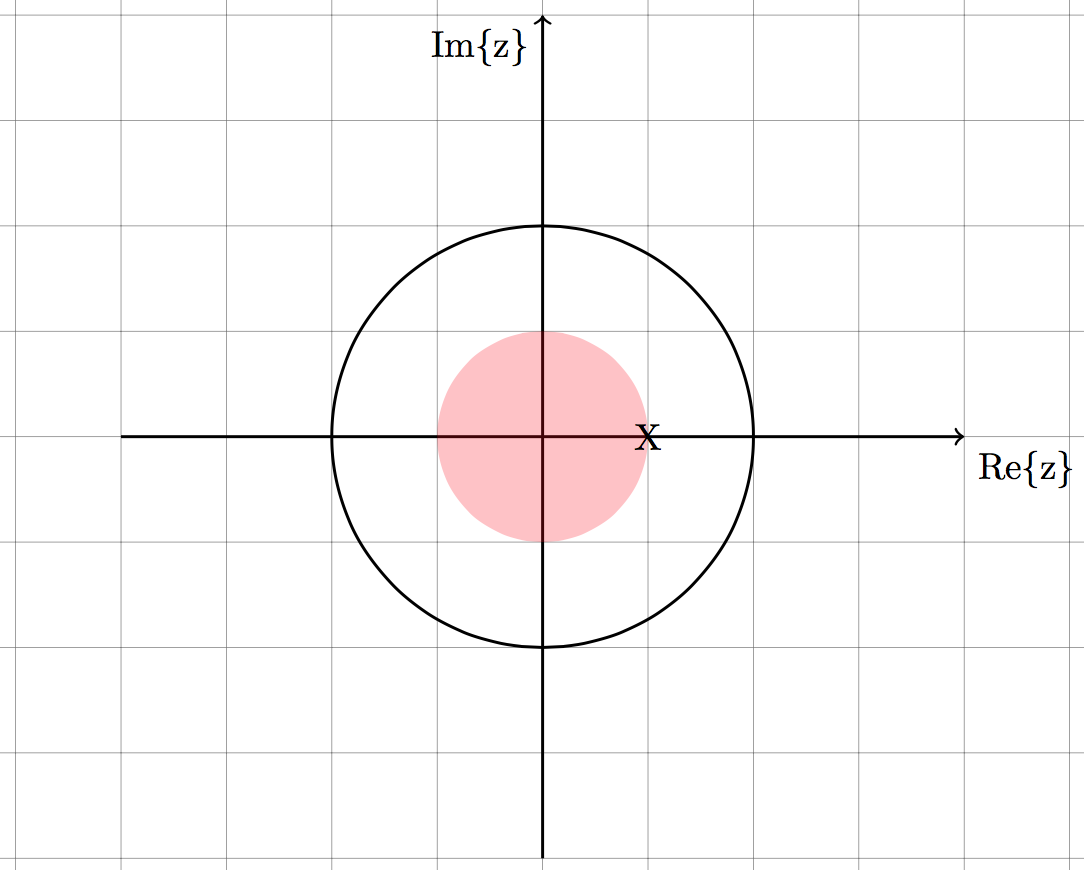
$$X(z) = \frac{1}{1-0.5z^{-1}}$$

1. Causal and Stable                                              2. Non-Causal and unstable

$x[n] = 0.5^nu[n]$                                                   $x[n] = -0.5^u[-n-1]$

Rule #1 and #5                                                        Rule #2

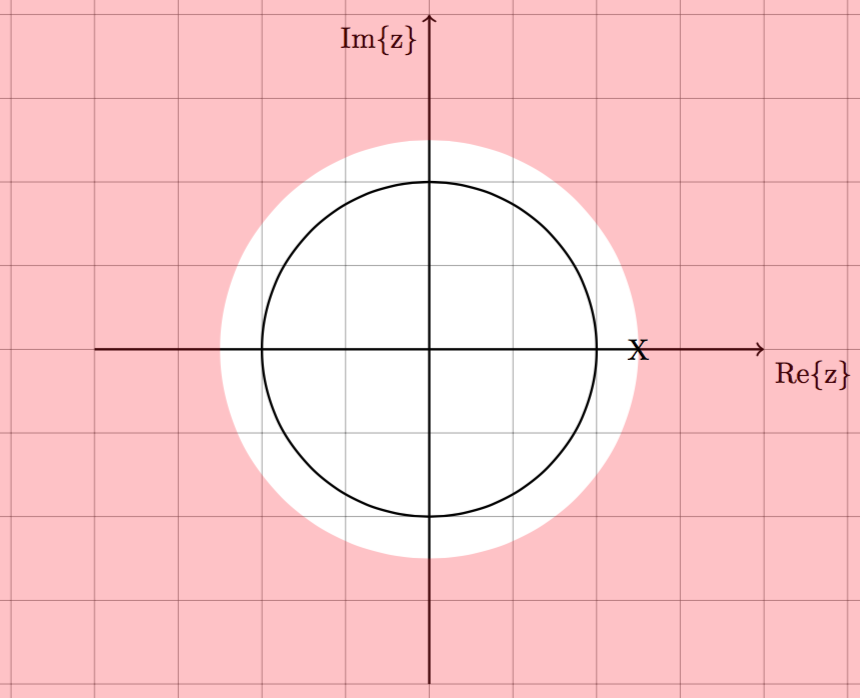
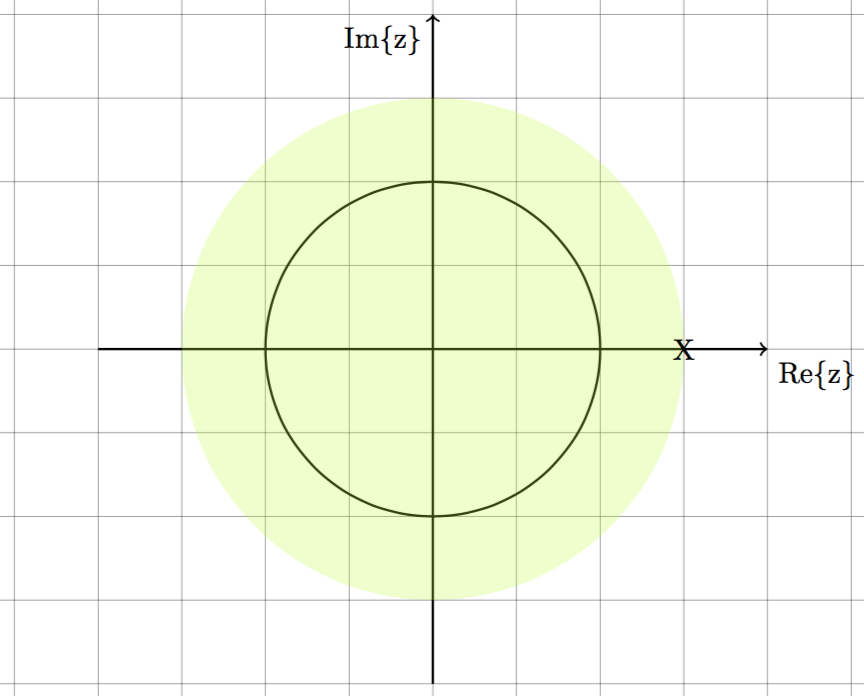
$$X(z) = \frac{1}{1-2z^{-1}}$$

1. Causal and unstable                                          2. Non-Causal and stable

$x[n] = 2^nu[n]$                                                       $x[n] = -2^u[-n-1]$

Rule #1                                                                    Rule #2 and #5

Multiple Pole System Example

$$ X(z) = \frac{1}{1-0.5z^{-1}} + \frac{1}{1-2z^{-1}} $$

This system has four possible ROC's, that is: there are four systems in the time domain that shares this z-transform.

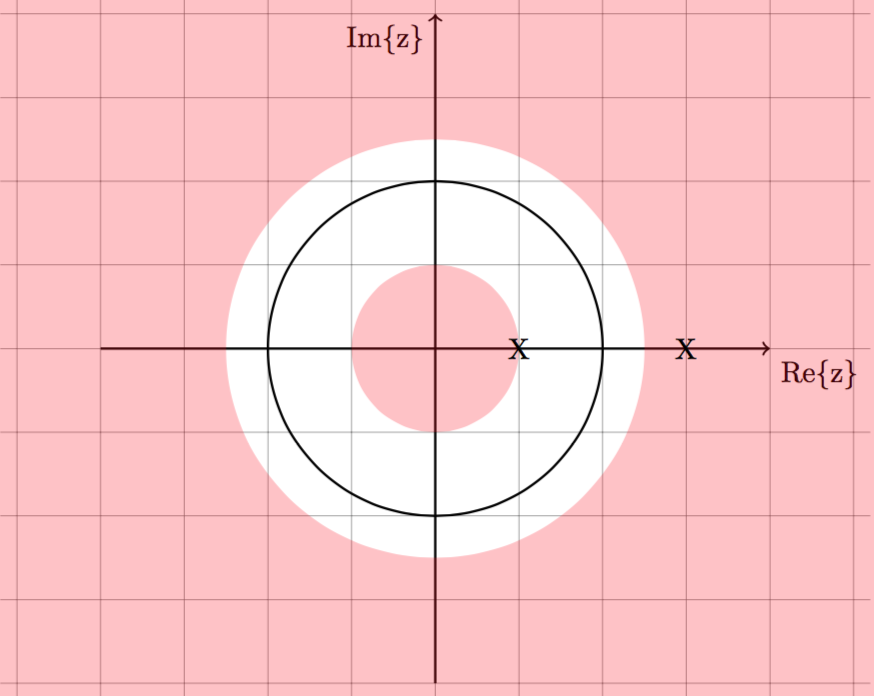
1. Causal: $$ x[n] = 0.5^nu[n] + 2^nu[n]$$

Rule #1 and #4

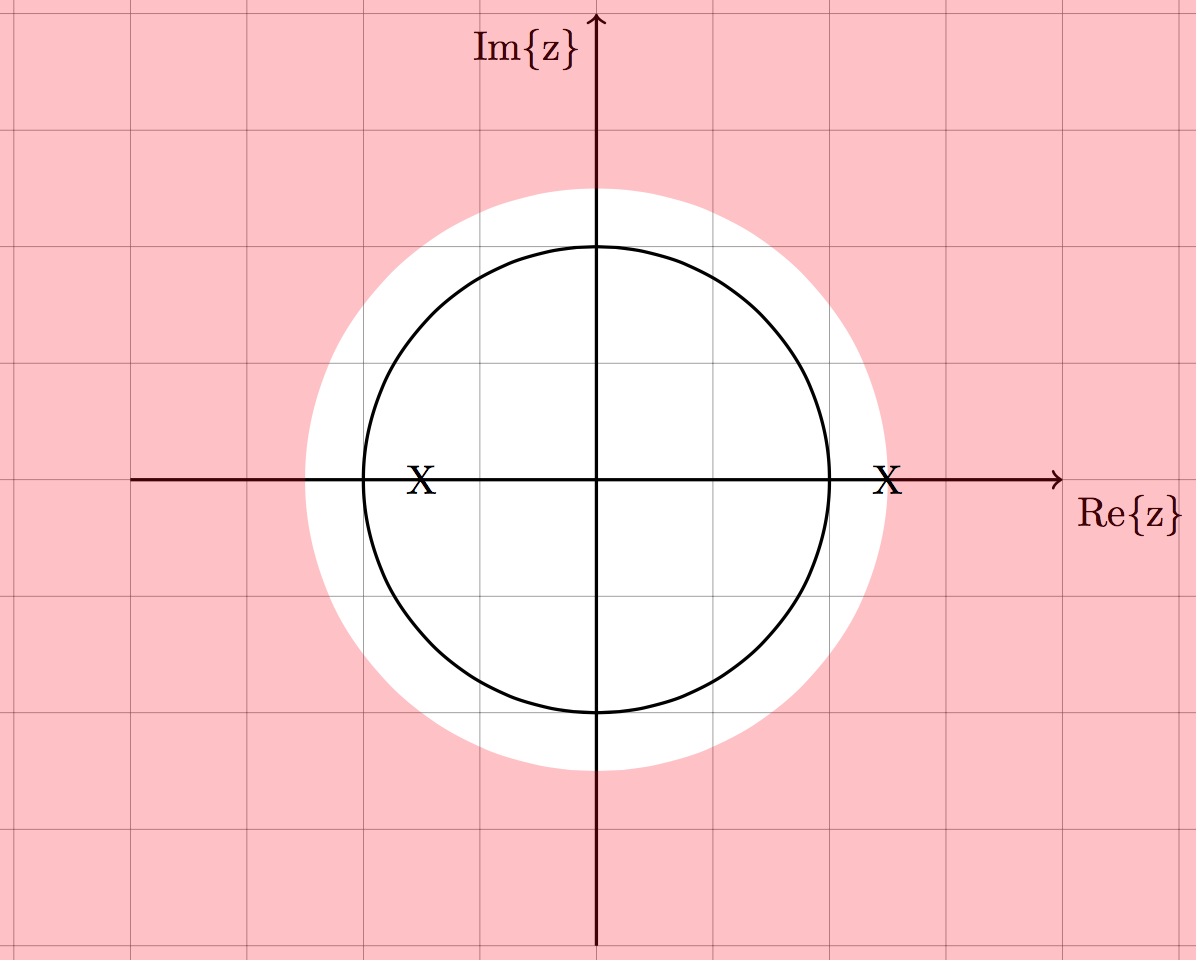
2. Non-causal $$x[n] = -0.5^nu[-n-1] - 2^nu[-n-1]$$

Rule #2 and #4

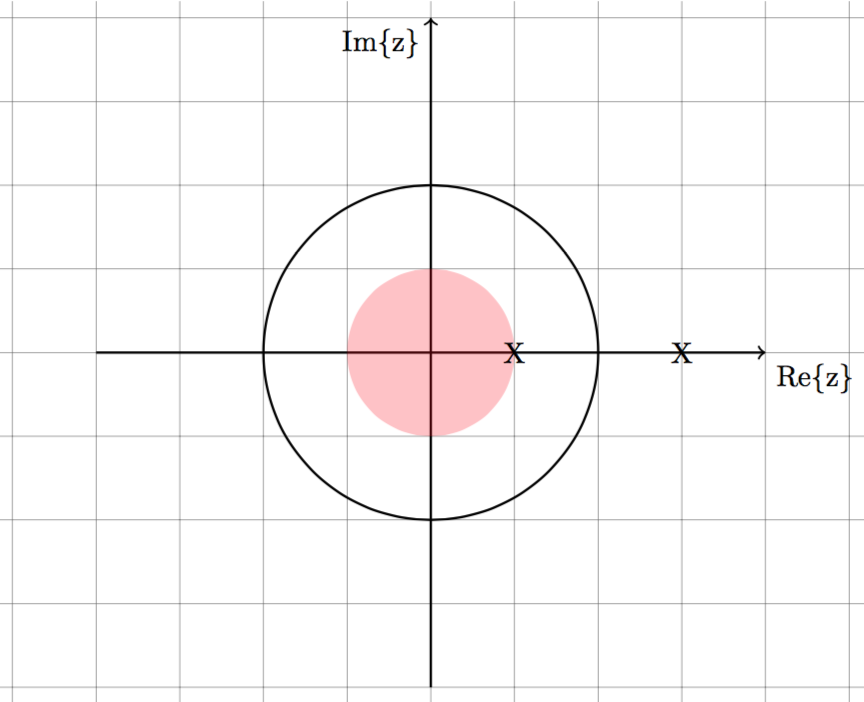
3. Two sided: $$x[n] = 0.5^nu[n] - 2^nu[-n-1]$$

Rule #3 and #5

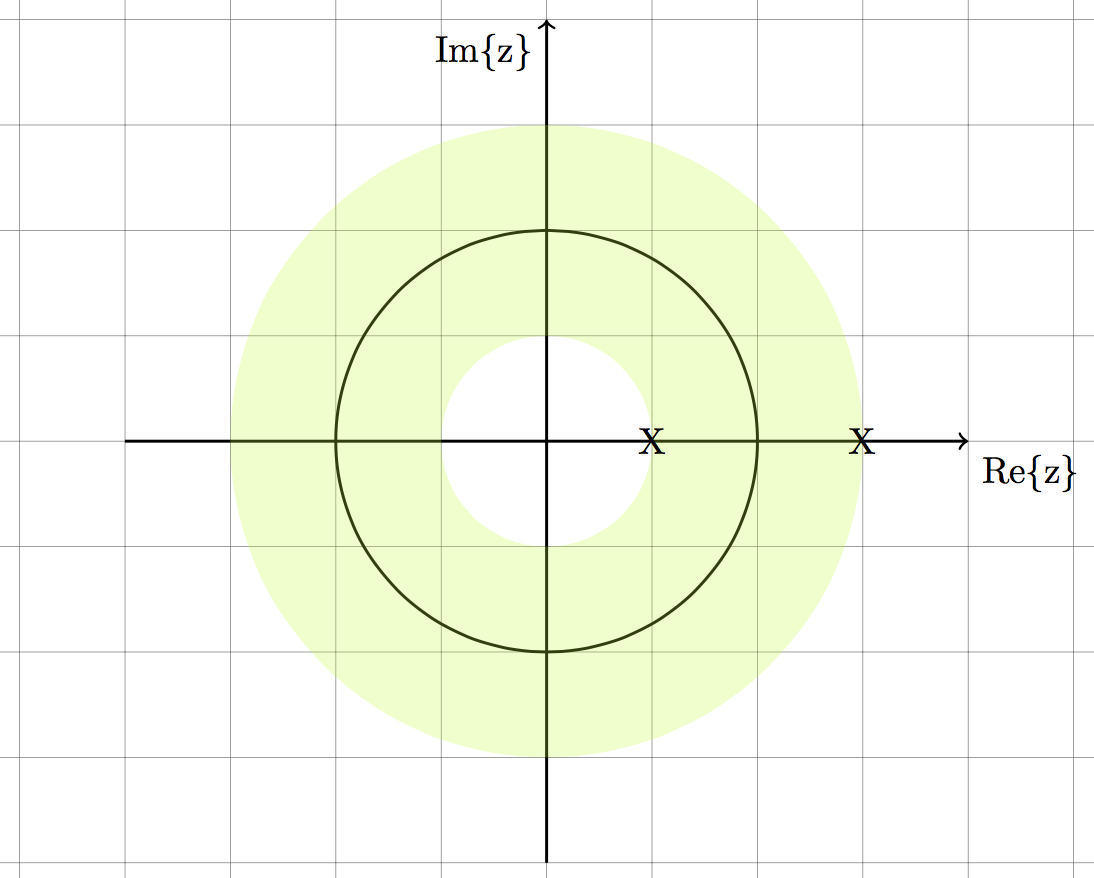
4. Two sided: $$x[n] = -0.5^nu[-n-1] + 2^nu[n]$$

Rule #3

Sign in