TMX Transmultiplexer (MATLAB Version)

This program executes a FDM (Frequency Division Multiplexion) via a Discrete Wavelet Transformation. It uses Daubechies filters.

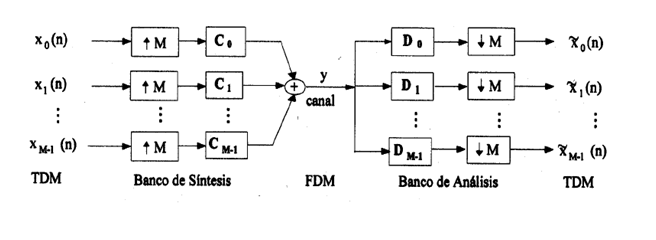
It has a step-by-step execution, in order to see the regeneration of the signal by each output branch. If you need any explanation please ask in the comment section.

A REFERENCE REPORT CAN BE FOUND AT:

http://www.box.net/shared/hca98fycuq

Please get the needed functions in the other code snippets below:

getsinc.m -> http://www.dsprelated.com/showcode/72.php

double2cfloat.m -> http://www.dsprelated.com/showcode/71.php

formafiltrosdwpt.m (TMX Integrated version) -> http://www.dsprelated.com/showcode/74.php

recorreder.m -> http://www.dsprelated.com/showcode/43.php

upsample2.m -> http://www.dsprelated.com/showcode/10.php

% UPIITA IPN 2010
% Procesamiento Digital de Señales
% Grupo 6TM1  Equipo #8
% Team members
%   Rogelio Baeza Nieves
%   Ponce Mosso Catarina
%   Valencia Pesqueira José David

% TMX Transmultiplexer -> Chain processing

close all;clear all;clc;

n_stages = 2;
n_branches = 2^n_stages;
dec_factor = 2^n_stages;
niter = 500;

N = 16;
input = zeros(2^n_stages,N);
for(k = 0:2^n_stages-1)
    input(k+1,:) = (1 + k * N ):((k+1)*N);
end
input;
in_cnt = 1;

typeofbasis = 'o';
typbior = 'bior2.2';
typor = 'db2';

if(typeofbasis == 'b')
    [Rf,Df] = biorwavf(typbior);
    [h0,h1,g0,g1] = biorfilt(Df,Rf);
elseif (typeofbasis == 'o')
    [h0,h1,g0,g1] = wfilters(typor);
end;

L = length(h0);

try
    sinc_factor = getsinc(n_stages,L) - 1;
catch
    disp('Error');
    return
end

for i = 1:1
hx = fliplr(formafiltrosdwpt(n_stages,2^n_stages,h0,h1));
Lhx = length(hx);
H = zeros(2^n_stages, Lhx);
for i=0:(2^n_stages)-1
    H(i+1,:)=fliplr(formafiltrosdwpt(n_stages,2^n_stages-i,h0,h1));
end
La = length(H(1,:));

G = zeros(2^n_stages, Lhx);
for i=0:(2^n_stages)-1
    G(i+1,:)=fliplr(formafiltrosdwpt(n_stages,2^n_stages-i,g0,g1));
end
Ls = length(G(1,:));

double2cfloat(H,'h', G,'g',sinc_factor);

analysisbuffer = zeros(1,La);

y = zeros(2^n_stages,1);

sbuffer = zeros(2^n_stages, Ls);
xnbuff = zeros(2^n_stages,1);
chanbuffer = [0];
outputbuffer = zeros(2^n_stages,1);
end

for i=1:niter %General iteration counter
    
    %% Synthesis stage
    i
    % Vector shifting (CLK/1)
    for j = 1:(2^n_stages)
        sbuffer(j,:) = recorreder(sbuffer(j,:),1);
    end
    
% Input interpolation
    if (mod(i,2^n_stages) == 1)&&(in_cnt<N-1)
        sbuffer(:,1) = input(:,in_cnt);
        in_cnt = in_cnt + 1;
    else
        sbuffer(:,1) = zeros(2^n_stages,1);
    end
    
    disp('inputs: ');
    disp(sbuffer)
    
    xnbuff = zeros(2^n_stages,1);
    for j=0:(2^n_stages)-1
        for k = 1 : Ls %convolution
            xnbuff(j+1,1) = xnbuff(j+1,1) + sbuffer(j+1,k)*G(j+1,k);
        end
    end
    
    chanbuffer = sum(xnbuff)   
    
    %% Analysis stage
    analysisbuffer = recorreder(analysisbuffer,1);    
    analysisbuffer(1)=chanbuffer;
    analysisbuffer;
   
    if (i>sinc_factor && mod(i-sinc_factor,2^n_stages) == 1)
    % If the counter is a multiply of the decimating factor, then compute
        y = zeros(2^n_stages,1);
        for j = 0:(2^n_stages)-1
            for k=1:La %convolución
                y(j+1,1) = y(j+1,1) + analysisbuffer(k)*H(j+1,k);
            end;
        end
        outputbuffer = y;
    end
    input;
    i
    outputbuffer
    pause;
end
  	return;