(So far, 231 people got it right out of 457 for a success rate of 50%)
(Thank you to Rick Lyons, author of the top-selling book Understanding Digital Signal Processing, for submitting this Quiz Question.)
Let's say a DSP practitioner performs a forward discrete Fourier transform (DFT), zero padding, and inverse DFT processing shown in the following figure.
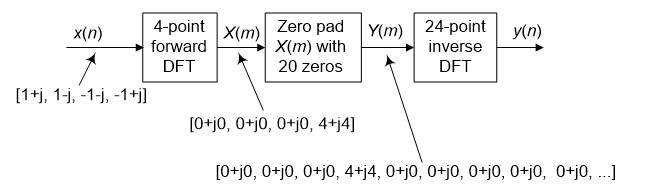
The x(n) input is a 4-sample negative-frequency complex exponential sequence, whose frequency is 1/4th its sample rate, defined by:
x(n) = [1+j, 1-j, -1-j, -1+j].
Quiz Question: The y(n) sequence will be
- Comments
- Write a Comment Select to add a comment

My Matlab routines:
function [Xk] = dfs(xn, N)
% Xk = DFS coeff. array over 0 <= k <= N-1
% xn = One period of periodic signal over 0 <= n <= N-1
% N = Fundamental period of xn
%
n = [0:1:N-1];
% row vector for n
k = [0:1:N-1];
% row vecor for k
WN = exp(-i*2*pi/N);
% Wn factor
nk = n'*k;
% creates a N by N matrix of nk values
WNnk = WN .^ nk;
% DFS matrix
Xk = xn * WNnk;
****************************************
function [xn] = idfs(Xk,N)
% Computes Inverse Discrete Fourier Series
% ----------------------------------------
% [xn] = idfs(Xk,N)
% xn = One period of periodic signal over 0 <= n <= N-1
% Xk = DFS coeff. array over 0 <= k <= N-1
% N = Fundamental period of Xk
%
n = [0:1:N-1];
% row vector for n
k = [0:1:N-1];
% row vecor for k
WN = exp(-i*2*pi/N);
% Wn factor
nk = n'*k;
% creates a N by N matrix of nk values
WNnk = WN .^ (-nk);
% IDFS matrix
xn = (Xk * WNnk)/N;
% row vector for IDFS values
**************************************************
function [xn]=pad(Xk,N)
xn=[Xk,zeros(1,N)]
*************************************************
function plotdfs(Xk)
%plot
N=length(Xk);
k=-N/2:N/2;
magXk = abs([Xk(N/2+1:N) Xk(1:N/2+1)]); % DFS magnitude
plot(k,magXk);
axis([-N/2,N/2,-0.5,5.5]);
xlabel("k"); ylabel("Xtilde(k)")
title("discrete Fourier transform (DFT) ")
******************************************************
my command lines:
X=[1+i, 1-i,-1-j,-1+i]
Xm=dfs(x,4)
Ym=pad(y,20)
y=idfs(ypad,24)
stem(0:23,real(y))
stem(0:23,imag(y))
dfsy=dfs(y,24)
plotdfs(dfsy)
I did it first :)
Keep 'em coming! Fun! Thanks, Rick Lyons!

Yip, I fell down that rabbit hole too - I saw pad and just assumed it meant what I expected it to mean and not the 'append' that is clearly illustrated in the problem. Next time I'll be more careful...nah, I'll just make some other silly mistake.
Score one for Mr. Lyons for the subtlety of this one.

Hi bbhattac. "Trick question"!! Who, me? Surely you're joking. :-)
(Actually, my Quiz Question originated from an e-mail I received recently from a young DSPer asking for help. The e-mailer was trying to perform time-domain interpolation by way of frequency-domain zero padding (more correctly called "zero stuffing").

Great one.
If you look at the mathematical expression for the IDFT, you could make the case that based on the formula, all the terms of the DFT represent a counter-clockwise rotating phase in time (positive frequency). In fact, all the terms are equally either positive frequencies OR negative frequencies given the circular nature of the DFT.
For example, one could argue that the original sequence in frequency [0 0 0 1] can also be a positive frequency exponential. Each of the n terms of the DFT (n being 0, 1,2, ...N-1, where N is the length of the DFT) represents either a positive frequency exponential, rotating n times counter-clockwise around the unit circle OR identically, rotating N-n time clock-wise around the unit circle. The DFT sequence [0 0 0 4] represents a phasor in time with magnitude 4 and starting angle 0 rotating 3 times around the unit circle in all cases of N = 4 or greater. When N =4 as in this case, the sequence [0 0 0 4] equally represents a phasor rotating 4-3 = 1 times clockwise around the unit circle. As we append zeros, we interpolate more samples of this same underlying time domain function; 3 rotations counter-clockwise. However in all these cases of adding zeros, there is still an equivalent negative frequency: If I add 20 zeros for N = 24, then the time domain function is a phasor rotating 3 times counter-clockwise (positive frequency) OR rotating 24-3 = 21 times clockwise (negative frequency)!
(This is similar to the equivalence of rotating clockwise 270° between 2 samples, or rotating counter-clockwise 90° - the result is the same - so given it is a sampled system with a many to one result, you can't really say it is rotating one way or the other).

Hi DanBoschen.
Although I didn't state it specifically (and it looks like I should have), the assumption with my original x(n) sequence is that it was sampled at a sample rate that satisfies the Nyquist Criterion. In which case x(n)'s complex-valued samples cannot rotate more than ±180 degrees from one sample to the next sample.
When that criterion is satisfied then there's no frequency ambiguity associated with x(n). The frequency of x(n) is negative 1/4th the sample rate.
What is a forward FFT?

it mean fft not inverse FFT :) if tell FFT may be better
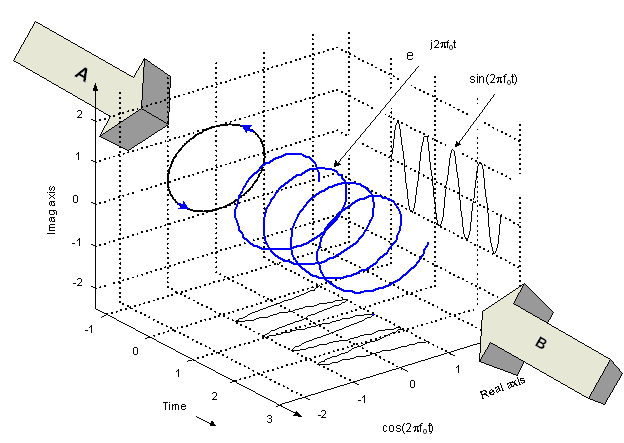
How to plot such a plot in matlab? for this quiz maybe usefull too.
@sh_honest: You can use plot3 function in matlab.
thanks yes i did it.
To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers:





















