Real Linear Filtering of Complex Signals

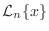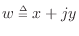When a filter is a linear filter (but not necessarily time-invariant), and its input is a complex signal , then, by linearity,

This means every linear filter maps complex signals to complex signals in a manner equivalent to applying the filter separately to the real and imaginary parts (which are each real). In other words, there is no ``interaction'' between the real and imaginary parts of a complex input signal when passed through a linear filter. If the filter is real, then filtering of complex signals can be carried out by simply performing real filtering on the real and imaginary parts separately (thereby avoiding complex arithmetic).

Appendix H presents a linear-algebraic view of linear filters that can be useful in certain applications.

---

Next Section:
Series Combination is Commutative
Previous Section:
Superposition:

Sign in