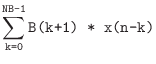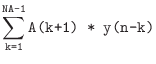DSPRelated.com
Free Books
The 2025 DSP Online Conference
   Free Books    Introduction to Digital Filters  

Software Implementation in Matlab

In Matlab or Octave, this type of filter can be implemented using the filter function. For example, the following matlab4.1 code computes the output signal y given the input signal x for a specific example comb filter: 

g1 = (0.5)^3;        % Some specific coefficients
g2 = (0.9)^5;
B = [1 0 0 g1];      % Feedforward coefficients, M1=3
A = [1 0 0 0 0 g2];  % Feedback coefficients, M2=5
N = 1000;            % Number of signal samples
x = rand(N,1);       % Random test input signal
y = filter(B,A,x);   % Matlab and Octave compatible
The example coefficients, $ g1 = 0.5^3 = 0.125$ and $ g2 = 0.9^5 = 0.59049$, are chosen to place all filter zeros at radius $ 0.5$ and all filter poles at radius $ 0.9$ in the complex $ z$ plane (as we shall see below).

The matlab filter function carries out the following computation for each element of the y array:

$\displaystyle \texttt{y(n)}$ $\displaystyle =$ $\displaystyle \sum_{\texttt{k=0}}^\texttt{NB-1} \texttt{B(k+1) * x(n-k)}$ (4.2)
  $\displaystyle -$ $\displaystyle \sum_{\texttt{k=1}}^\texttt{NA-1} \texttt{A(k+1) * y(n-k)} \protect$ (4.3)

for $ \texttt{n}=1,2,\dots,\texttt{N}$, where NA = length(A) and NB = length(B). Note that the indices of x and y can go negative in this expression. By default, such terms are replaced by zero. However, the filter function has an optional fourth argument for specifying the initial state of the filter, which includes past input and past output samples seen by the filter. This argument is used to forward the filter's state across successive blocks of data:
[y1,state] = filter(B,A,x1);       % filter 1st block x1
[y2,state] = filter(B,A,x2,state); % filter 2nd block x2
...

Sample-Level Implementation in Matlab

For completeness, a direct matlab implementation of the built-in filter function (Eq.$ \,$(3.3)) is given in Fig.3.2. While this code is useful for study, it is far slower than the built-in filter function. As a specific example, filtering $ 10,000$ samples of data using an order 100 filter on a 900MHz Athlon PC required 0.01 seconds for filter and 10.4 seconds for filterslow. Thus, filter was over a thousand times faster than filterslow in this case. The complete test is given in the following matlab listing:

x = rand(10000,1); % random input signal
B = rand(101,1);   % random coefficients
A = [1;0.001*rand(100,1)]; % random but probably stable
tic; yf=filter(B,A,x); ft=toc
tic; yfs=filterslow(B,A,x); fst=toc
The execution times differ greatly for two reasons:
  1. recursive feedback cannot be ``vectorized'' in general, and
  2. built-in functions such as filter are written in C, precompiled, and linked with the main program.

Figure 3.2: Matlab function for implementing a digital filter directly. Do not use this in practice because it is much slower than the built-in filter routine.
  
function [y] = filterslow(B,A,x)
% FILTERSLOW: Filter x to produce y = (B/A) x .
%       Equivalent to 'y = filter(B,A,x)' using
%       a slow (but tutorial) method.

NB = length(B);
NA = length(A);
Nx = length(x);

xv = x(:); % ensure column vector

% do the FIR part using vector processing:
v = B(1)*xv;
if NB>1
  for i=2:min(NB,Nx)
    xdelayed = [zeros(i-1,1); xv(1:Nx-i+1)];
    v = v + B(i)*xdelayed;
  end;
end; % fir part done, sitting in v

% The feedback part is intrinsically scalar,
% so this loop is where we spend a lot of time.
y = zeros(length(x),1); % pre-allocate y
ac = - A(2:NA);
for i=1:Nx, % loop over input samples
  t=v(i);   % initialize accumulator
  if NA>1,
    for j=1:NA-1
      if i>j,
        t=t+ac(j)*y(i-j);
      %else y(i-j) = 0
      end;
    end;
  end;
  y(i)=t;
end;

y = reshape(y,size(x)); % in case x was a row vector

Next Section:
Software Implementation in C++
Previous Section:
Signal Flow Graph
The 2025 DSP Online Conference