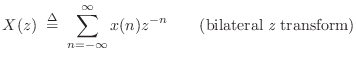The Z Transform
The bilateral z transform of the discrete-time signal ![]() is
defined to be
is
defined to be
where
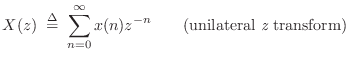 |
(7.2) |
The unilateral z transform is most commonly used. For inverting z transforms, see §6.8.
Recall (§4.1) that the mathematical representation of a
discrete-time signal ![]() maps each integer
maps each integer
![]() to a complex
number (
to a complex
number (
![]() ) or real number (
) or real number (
![]() ). The z transform
of
). The z transform
of ![]() , on the other hand,
, on the other hand, ![]() , maps every complex number
, maps every complex number
![]() to a new complex number
to a new complex number
![]() . On a higher
level, the z transform, viewed as a linear operator, maps an entire
signal
. On a higher
level, the z transform, viewed as a linear operator, maps an entire
signal ![]() to its z transform
to its z transform ![]() . We think of this as a ``function to
function'' mapping. We may say
. We think of this as a ``function to
function'' mapping. We may say ![]() is the z transform of
is the z transform of ![]() by writing
by writing
The z transform of a signal ![]() can be regarded as a polynomial in
can be regarded as a polynomial in
![]() , with coefficients given by the signal samples. For example,
the signal
, with coefficients given by the signal samples. For example,
the signal
![$\displaystyle x(n) = \left\{\begin{array}{ll}
n+1, & 0\leq n \leq 2 \\ [5pt]
0, & \mbox{otherwise} \\
\end{array}\right.
$](http://www.dsprelated.com/josimages_new/filters/img633.png)
Next Section:
Existence of the Z Transform
Previous Section:
Time Domain Representation Problems