Free Books    Mathematics of the DFT  

Bluestein's FFT Algorithm

Like Rader's FFT, Bluestein's FFT algorithm (also known as the chirp $ z$-transform algorithm), can be used to compute prime-length DFTs in $ {\cal O}(N\lg N)$ operations [24, pp. 213-215].A.6 However, unlike Rader's FFT, Bluestein's algorithm is not restricted to prime lengths, and it can compute other kinds of transforms, as discussed further below.

Beginning with the DFT

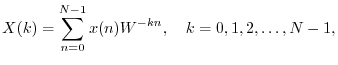
$\displaystyle X(k) = \sum_{n=0}^{N-1} x(n) W^{-kn}, \quad k=0,1,2,\ldots,N-1, $

where $ W \isdeftext \exp(j2\pi/N)$ denotes a primitive $ N$th root of unity,A.7 we multiply and divide by $ W^{(n^2+k^2)/2}$ to obtain

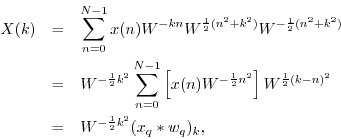
\begin{eqnarray*} X(k) &=& \sum_{n=0}^{N-1}x(n)W^{-kn}W^{\frac{1}{2}(n^2+k^2)}... ...frac{1}{2}(k-n)^2} \\ &=& W^{-\frac{1}{2}k^2} (x_q \ast w_q)_k, \end{eqnarray*}

where `$ \ast $' denotes convolution (§7.2.4), and the sequences $ x_q$ and $ w_q$ are defined by

\begin{eqnarray*} x_q(n) & \isdef & x(n)W^{-\frac{1}{2}n^2}, \quad n=0,1,2,\ldot... ...{\frac{1}{2}n^2}, \quad n=-N+1,-N+2,\ldots,-1,0,1,2,\ldots, N-1, \end{eqnarray*}

where the ranges of $ n$ given are those actually required by the convolution sum above. Beyond these required minimum ranges for $ n$, the sequences may be extended by zeros. As a result, we may implement this convolution (which is cyclic for even $ N$ and ``negacyclic'' for odd $ N$) using zero-padding and a larger cyclic convolution, as mentioned in §7.2.4. In particular, the larger cyclic convolution size $ N_2\ge 2N-1$ may be chosen a power of 2, which need not be larger than $ 4N-3$. Within this larger cyclic convolution, the negative-$ n$ indexes map to $ N_2-N+1:N_2-1$ in the usual way.

Note that the sequence $ x_q(n)$ above consists of the original data sequence $ x(n)$ multiplied by a signal $ \exp(j\pi n^2/N)$ which can be interpreted as a sampled complex sinusoid with instantaneous normalized radian frequency $ 2\pi n/N$, i.e., an instantaneous frequency that increases linearly with time. Such signals are called chirp signals. For this reason, Bluestein's algorithm is also called the chirp $ z$-transform algorithm [59].

In summary, Bluestein's FFT algorithm provides complexity $ N \lg N$ for any positive integer DFT-length $ N$ whatsoever, even when $ N$ is prime.

Other adaptations of the Bluestein FFT algorithm can be used to compute a contiguous subset of DFT frequency samples (any uniformly spaced set of samples along the unit circle), with $ N \lg N$ complexity. It can similarly compute samples of the $ z$ transform along a sampled spiral of the form $ z^k$, where $ z$ is any complex number, and $ k=k_0,k_0+1,\ldots,k_0+N-1$, again with complexity $ N \lg N$ [24].

Next Section:
Fast Transforms in Audio DSP
Previous Section:
Rader's FFT Algorithm for Prime Lengths