Free Books    Mathematics of the DFT  

Convolution

The convolution of two signals $ x$ and $ y$ in $ {\bf C}^N$ may be denoted `` $ x\circledast y$'' and defined by

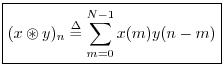
$\displaystyle \zbox {(x\circledast y)_n \isdef \sum_{m=0}^{N-1}x(m) y(n-m)} $

Note that this is circular convolution (or ``cyclic'' convolution).7.4 The importance of convolution in linear systems theory is discussed in §8.3.

Cyclic convolution can be expressed in terms of previously defined operators as

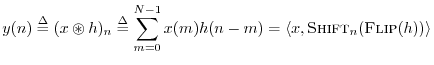
$\displaystyle y(n) \isdef (x\circledast h)_n \isdef \sum_{m=0}^{N-1}x(m)h(n-m) = \left<x,\hbox{\sc Shift}_n(\hbox{\sc Flip}(h))\right>$   $\displaystyle \mbox{($h$\ real)}$

where $ x,y\in{\bf C}^N$ and $ h\in{\bf R}^N$. This expression suggests graphical convolution, discussed below in §7.2.4.

Commutativity of Convolution

Convolution (cyclic or acyclic) is commutative, i.e.,

$\displaystyle \zbox {x\circledast y = y\circledast x .} $


Proof:

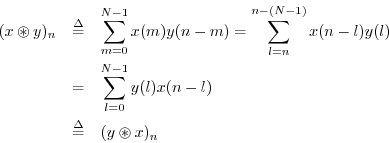
\begin{eqnarray*} (x\circledast y)_n &\isdef & \sum_{m=0}^{N-1}x(m) y(n-m) = \s... ...=& \sum_{l=0}^{N-1}y(l) x(n-l) \\ &\isdef & (y \circledast x)_n \end{eqnarray*}

In the first step we made the change of summation variable $ l\isdeftext n-m$, and in the second step, we made use of the fact that any sum over all $ N$ terms is equivalent to a sum from 0 to $ N-1$.

Convolution as a Filtering Operation

In a convolution of two signals $ x\circledast y$, where both $ x$ and $ y$ are signals of length $ N$ (real or complex), we may interpret either $ x$ or $ y$ as a filter that operates on the other signal which is in turn interpreted as the filter's ``input signal''.7.5 Let $ h\in{\bf C}^N$ denote a length $ N$ signal that is interpreted as a filter. Then given any input signal $ x\in{\bf C}^N$, the filter output signal $ y\in{\bf C}^N$ may be defined as the cyclic convolution of $ x$ and $ h$:

$\displaystyle y = h\circledast x = x \circledast h $

Because the convolution is cyclic, with $ x$ and $ h$ chosen from the set of (periodically extended) vectors of length $ N$, $ h(n)$ is most precisely viewed as the impulse-train-response of the associated filter at time $ n$. Specifically, the impulse-train response $ h\in{\bf C}^N$ is the response of the filter to the impulse-train signal $ \delta\isdeftext [1,0,\ldots,0]\in{\bf R}^N$, which, by periodic extension, is equal to

$\displaystyle \delta(n) = \left\{\begin{array}{ll} 1, & n=0\;\mbox{(mod $N$)} \\ [5pt] 0, & n\ne 0\;\mbox{(mod $N$)}. \\ \end{array} \right. $

Thus, $ N$ is the period of the impulse-train in samples--there is an ``impulse'' (a `$ 1$') every $ N$ samples. Neglecting the assumed periodic extension of all signals in $ {\bf C}^N$, we may refer to $ \delta$ more simply as the impulse signal, and $ h$ as the impulse response (as opposed to impulse-train response). In contrast, for the DTFT (§B.1), in which the discrete-time axis is infinitely long, the impulse signal $ \delta(n)$ is defined as

$\displaystyle \delta(n) \isdef \left\{\begin{array}{ll} 1, & n=0 \\ [5pt] 0, & n\ne 0 \\ \end{array} \right. $

and no periodic extension arises.

As discussed below (§7.2.7), one may embed acyclic convolution within a larger cyclic convolution. In this way, real-world systems may be simulated using fast DFT convolutions (see Appendix A for more on fast convolution algorithms).

Note that only linear, time-invariant (LTI) filters can be completely represented by their impulse response (the filter output in response to an impulse at time 0). The convolution representation of LTI digital filters is fully discussed in Book II [68] of the music signal processing book series (in which this is Book I).

Convolution Example 1: Smoothing a Rectangular Pulse

Figure 7.3: Illustration of the convolution of a rectangular pulse $ x=[0 ,0 ,0 ,0,1,1,1,1,1,1,0,0,0,0]$ and the impulse response of an ``averaging filter'' $ h=[1/3,1/3,1/3,0,0,0,0,0,0,0,0,0,0,0]$ ($ N=14$).
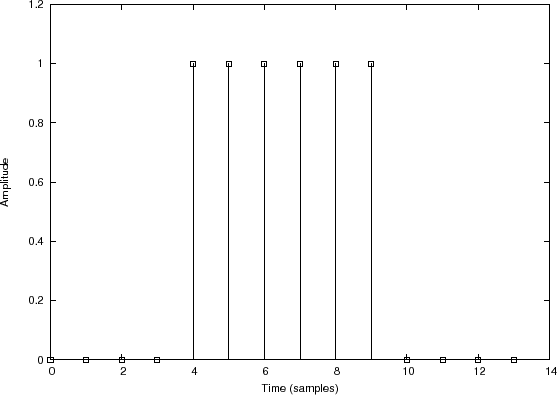
\includegraphics{eps/smoother-x}
Filter input signal 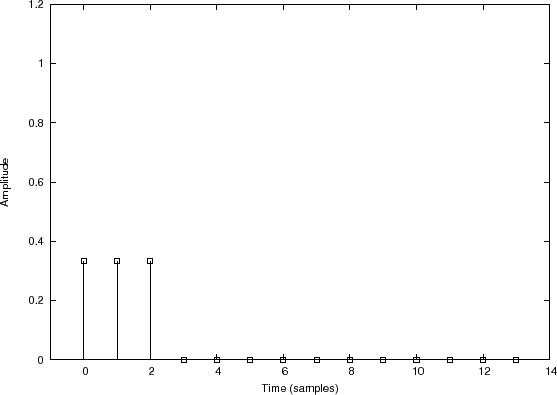$ x(n)$.

\includegraphics{eps/smoother-h}
Filter impulse response 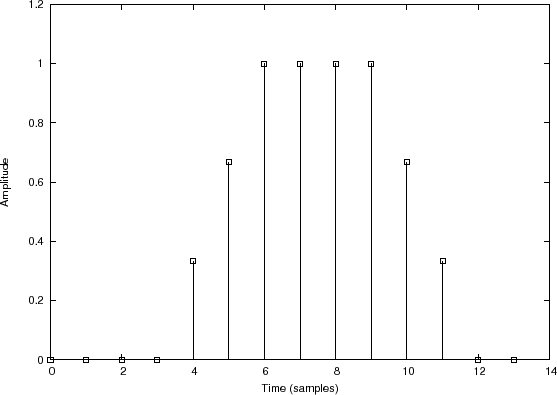$ h(n)$.

\includegraphics{eps/smoother-y}
Filter output signal $ y(n)$.

Figure 7.3 illustrates convolution of

$\displaystyle x = [ 0, 0, 0,0,1,1,1,1,1,1,0,0,0,0] $

with

$\displaystyle h = \left[\frac{1}{3},\frac{1}{3},\frac{1}{3},0,0,0,0,0,0,0,0,0,0,0\right] $

to get

$\displaystyle y = x\circledast h = \left[0,0,0,0,\frac{1}{3},\frac{2}{3},1,1,1,1,\frac{2}{3},\frac{1}{3},0,0\right] \protect$ (7.2)

as graphed in Fig.7.3(c). In this case, $ h$ can be viewed as a ``moving three-point average'' filter. Note how the corners of the rectangular pulse are ``smoothed'' by the three-point filter. Also note that the pulse is smeared to the ``right'' (forward in time) because the filter impulse response starts at time zero. Such a filter is said to be causal (see [68] for details). By shifting the impulse response left one sample to get

$\displaystyle h=\left[\frac{1}{3},\frac{1}{3},0,0,0,0,0,0,0,0,0,0,\frac{1}{3}\right] $

(in which case $ \hbox{\sc Flip}(h)=h$), we obtain a noncausal filter $ h$ which is symmetric about time zero so that the input signal is smoothed ``in place'' with no added delay (imagine Fig.7.3(c) shifted left one sample, in which case the input pulse edges align with the midpoint of the rise and fall in the output signal).

Convolution Example 2: ADSR Envelope

Figure 7.4: Illustration of the convolution of two rectangular pulses with a truncated exponential impulse response.
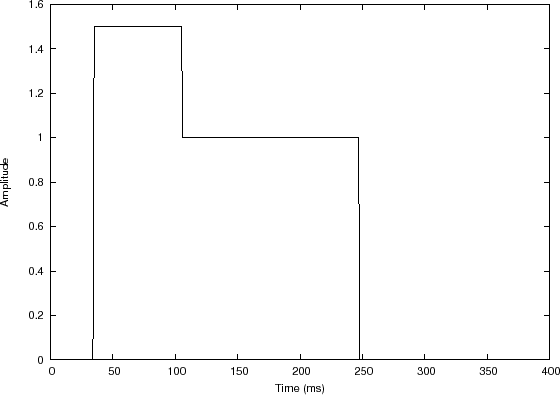
\includegraphics{eps/adsr-x}
Filter input signal $ x(n)$.

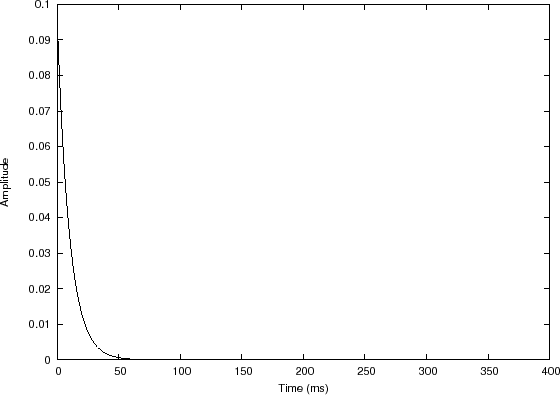
\includegraphics{eps/adsr-h}
Filter impulse response 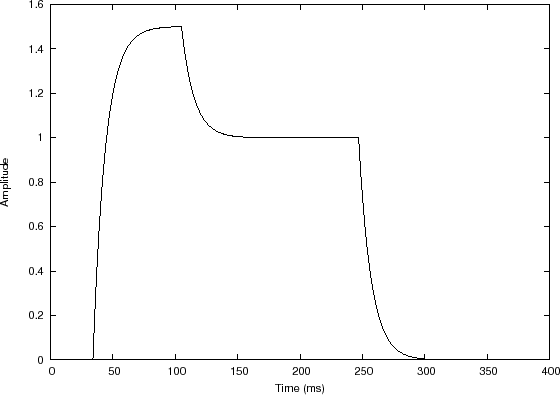$ h(n)$.

\includegraphics{eps/adsr-y}
Filter output signal $ y(n)$.

In this example, the input signal is a sequence of two rectangular pulses, creating a piecewise constant function, depicted in Fig.7.4(a). The filter impulse response, shown in Fig.7.4(b), is a truncated exponential.7.6

In this example, $ h$ is again a causal smoothing-filter impulse response, and we could call it a ``moving weighted average'', in which the weighting is exponential into the past. The discontinuous steps in the input become exponential ``asymptotes'' in the output which are approached exponentially. The overall appearance of the output signal resembles what is called an attack, decay, release, and sustain envelope, or ADSR envelope for short. In a practical ADSR envelope, the time-constants for attack, decay, and release may be set independently. In this example, there is only one time constant, that of $ h$. The two constant levels in the input signal may be called the attack level and the sustain level, respectively. Thus, the envelope approaches the attack level at the attack rate (where the ``rate'' may be defined as the reciprocal of the time constant), it next approaches the sustain level at the ``decay rate'', and finally, it approaches zero at the ``release rate''. These envelope parameters are commonly used in analog synthesizers and their digital descendants, so-called virtual analog synthesizers. Such an ADSR envelope is typically used to multiply the output of a waveform oscillator such as a sawtooth or pulse-train oscillator. For more on virtual analog synthesis, see, for example, [78,77].

Convolution Example 3: Matched Filtering

Figure 7.5: Illustration of convolution of $ y=[1,1,1,1,0,0,0,0]$ and ``matched filter'' $ h=\protect\hbox{\sc Flip}(y)=[1,0,0,0,0,1,1,1]$ ($ N=8$).
\includegraphics[width=2.5in]{eps/conv}

Figure 7.5 illustrates convolution of

\begin{eqnarray*} y&=&[1,1,1,1,0,0,0,0] \\ h&=&[1,0,0,0,0,1,1,1] \end{eqnarray*}

to get

$\displaystyle y\circledast h = [4,3,2,1,0,1,2,3]. \protect$ (7.3)

For example, $ y$ could be a ``rectangularly windowed signal, zero-padded by a factor of 2,'' where the signal happened to be dc (all $ 1$s). For the convolution, we need

$\displaystyle \hbox{\sc Flip}(h) = [1,1,1,1,0,0,0,0] $

which is the same as $ y$. When $ h=\hbox{\sc Flip}(y)$, we say that $ h$ is a matched filter for $ y$.7.7 In this case, $ h$ is matched to look for a ``dc component,'' and also zero-padded by a factor of $ 2$. The zero-padding serves to simulate acyclic convolution using circular convolution. Note from Eq.$ \,$(7.3) that the maximum is obtained in the convolution output at time 0. This peak (the largest possible if all input signals are limited to $ [-1,1]$ in magnitude), indicates the matched filter has ``found'' the dc signal starting at time 0. This peak would persist in the presence of some amount of noise and/or interference from other signals. Thus, matched filtering is useful for detecting known signals in the presence of noise and/or interference [34].

Graphical Convolution

As mentioned above, cyclic convolution can be written as

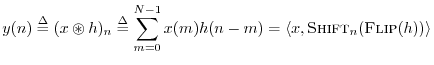
$\displaystyle y(n) \isdef (x\circledast h)_n \isdef \sum_{m=0}^{N-1}x(m)h(n-m) = \left<x,\hbox{\sc Shift}_n(\hbox{\sc Flip}(h))\right>$   $\displaystyle \mbox{($h$\ real)}$

where $ x,y\in{\bf C}^N$ and $ h\in{\bf R}^N$. It is instructive to interpret this expression graphically, as depicted in Fig.7.5 above. The convolution result at time $ n=0$ is the inner product of $ x$ and $ \hbox{\sc Flip}(h)$, or $ y(0)=\left<x,\hbox{\sc Flip}(h)\right>$. For the next time instant, $ n=1$, we shift $ \hbox{\sc Flip}(h)$ one sample to the right and repeat the inner product operation to obtain $ y(1)=\left<x,\hbox{\sc Shift}_1(\hbox{\sc Flip}(h))\right>$, and so on. To capture the cyclic nature of the convolution, $ x$ and $ \hbox{\sc Shift}_n(\hbox{\sc Flip}(h))$ can be imagined plotted on a cylinder. Thus, Fig.7.5 shows the cylinder after being ``cut'' along the vertical line between $ n=N-1$ and $ n=0$ and ``unrolled'' to lay flat.

Polynomial Multiplication

Note that when you multiply two polynomials together, their coefficients are convolved. To see this, let $ p(x)$ denote the $ m$th-order polynomial

$\displaystyle p(x) = p_0 + p_1 x + p_2 x^2 + \cdots + p_m x^m $

with coefficients $ p_i$, and let $ q(x)$ denote the $ n$th-order polynomial

$\displaystyle q(x) = q_0 + q_1 x + q_2 x^2 + \cdots + q_n x^n $

with coefficients $ q_i$. Then we have [1]

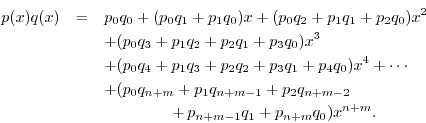
\begin{eqnarray*} p(x) q(x) &=& p_0 q_0 + (p_0 q_1 + p_1 q_0) x + (p_0 q_2 + p_1... ...\qquad\qquad\; \mathop{+} p_{n+m-1} q_1 + p_{n+m} q_0) x^{n+m}. \end{eqnarray*}

Denoting $ p(x) q(x)$ by

$\displaystyle r(x) \isdef p(x) q(x) = r_0 + r_1 x + r_2 x^2 + \cdots + r_{m+n} x^{m+n}, $

we have that the $ i$th coefficient can be expressed as

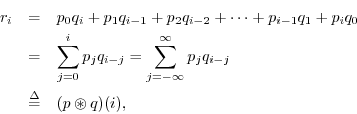
\begin{eqnarray*} r_i &=& p_0 q_i + p_1 q_{i-1} + p_2 q_{i-2} + \cdots + p_{i-1}... ...=-\infty}^\infty p_j q_{i-j}\\ &\isdef & (p \circledast q)(i), \end{eqnarray*}

where $ p_i$ and $ q_i$ are doubly infinite sequences, defined as zero for $ i<0$ and $ i>m,n$, respectively.

Multiplication of Decimal Numbers

Since decimal numbers are implicitly just polynomials in the powers of 10, e.g.,

$\displaystyle 3819 = 3\cdot 10^3 + 8\cdot 10^2 + 1\cdot 10^1 + 9\cdot 10^0, $

it follows that multiplying two numbers convolves their digits. The only twist is that, unlike normal polynomial multiplication, we have carries. That is, when a convolution result (output digit) exceeds 10, we subtract 10 from the result and add 1 to the digit in the next higher place.

Next Section:
Correlation
Previous Section:
Shift Operator