Free Books    Mathematics of the DFT  

Conjugation and Reversal


Theorem: For any $ x\in{\bf C}^N$,

$\displaystyle \zbox {\overline{x} \;\longleftrightarrow\;\hbox{\sc Flip}(\overline{X}).} $


Proof:

\begin{eqnarray*} \hbox{\sc DFT}_k(\overline{x}) &\isdef & \sum_{n=0}^{N-1}\ov... ...n) e^{-j 2\pi n(-k)/N}} \isdef \hbox{\sc Flip}_k(\overline{X}) \end{eqnarray*}


Theorem: For any $ x\in{\bf C}^N$,

$\displaystyle \zbox {\hbox{\sc Flip}(\overline{x}) \;\longleftrightarrow\;\overline{X}.} $


Proof: Making the change of summation variable $ m\isdeftext N-n$, we get

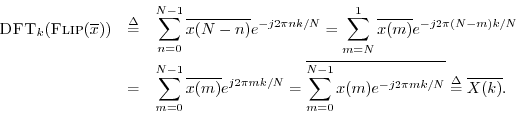
\begin{eqnarray*} \hbox{\sc DFT}_k(\hbox{\sc Flip}(\overline{x})) &\isdef & \s... ...sum_{m=0}^{N-1}x(m) e^{-j 2\pi m k/N}} \isdef \overline{X(k)}. \end{eqnarray*}


Theorem: For any $ x\in{\bf C}^N$,

$\displaystyle \zbox {\hbox{\sc Flip}(x) \;\longleftrightarrow\;\hbox{\sc Flip}(X).} $


Proof:

\begin{eqnarray*} \hbox{\sc DFT}_k[\hbox{\sc Flip}(x)] &\isdef & \sum_{n=0}^{N-1... ...-1}x(m) e^{j 2\pi mk/N} \isdef X(-k) \isdef \hbox{\sc Flip}_k(X) \end{eqnarray*}

Corollary: For any $ x\in{\bf R}^N$,

$\displaystyle \zbox {\hbox{\sc Flip}(x) \;\longleftrightarrow\;\overline{X}}$   $\displaystyle \mbox{($x$\ real).}$


Proof: Picking up the previous proof at the third formula, remembering that $ x$ is real,

$\displaystyle \sum_{m=0}^{N-1}x(m) e^{j 2\pi mk/N} = \overline{\sum_{m=0}^{N-1}... .../N}} = \overline{\sum_{m=0}^{N-1}x(m) e^{-j 2\pi mk/N}} \isdef \overline{X(k)} $

when $ x(m)$ is real.

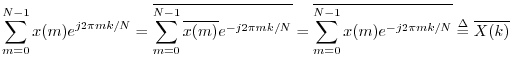
Thus, conjugation in the frequency domain corresponds to reversal in the time domain. Another way to say it is that negating spectral phase flips the signal around backwards in time.

Corollary: For any $ x\in{\bf R}^N$,

$\displaystyle \zbox {\hbox{\sc Flip}(X) = \overline{X}}$   $\displaystyle \mbox{($x$\ real).}$


Proof: This follows from the previous two cases.


Definition: The property $ X(-k)=\overline{X(k)}$ is called Hermitian symmetry or ``conjugate symmetry.'' If $ X(-k)=-\overline{X(k)}$, it may be called skew-Hermitian.

Another way to state the preceding corollary is

$\displaystyle \zbox {x\in{\bf R}^N\;\longleftrightarrow\;X\;\mbox{is Hermitian}.} $

Next Section:
Symmetry
Previous Section:
Linearity