Symmetry
In the previous section, we found
![]() when
when ![]() is
real. This fact is of high practical importance. It says that the
spectrum of every real signal is Hermitian.
Due to this symmetry, we may discard all negative-frequency spectral
samples of a real signal and regenerate them later if needed from the
positive-frequency samples. Also, spectral plots of real signals are
normally displayed only for positive frequencies; e.g., spectra of
sampled signals are normally plotted over the range 0 Hz to
is
real. This fact is of high practical importance. It says that the
spectrum of every real signal is Hermitian.
Due to this symmetry, we may discard all negative-frequency spectral
samples of a real signal and regenerate them later if needed from the
positive-frequency samples. Also, spectral plots of real signals are
normally displayed only for positive frequencies; e.g., spectra of
sampled signals are normally plotted over the range 0 Hz to ![]() Hz. On the other hand, the spectrum of a complex signal must
be shown, in general, from
Hz. On the other hand, the spectrum of a complex signal must
be shown, in general, from ![]() to
to ![]() (or from 0 to
(or from 0 to ![]() ),
since the positive and negative frequency components of a complex
signal are independent.
),
since the positive and negative frequency components of a complex
signal are independent.
Recall from §7.3 that a signal ![]() is said to be
even if
is said to be
even if
![]() , and odd if
, and odd if
![]() . Below
are are Fourier theorems pertaining to even and odd signals and/or
spectra.
. Below
are are Fourier theorems pertaining to even and odd signals and/or
spectra.
Theorem: If
![]() , then
re
, then
re![]() is even and
im
is even and
im![]() is odd.
is odd.
Proof: This follows immediately from the conjugate symmetry of ![]() for real signals
for real signals
![]() .
.
Theorem: If
![]() ,
,
![]() is even and
is even and ![]() is odd.
is odd.
Proof: This follows immediately from the conjugate symmetry of ![]() expressed
in polar form
expressed
in polar form
![]() .
.
The conjugate symmetry of spectra of real signals is perhaps the most important symmetry theorem. However, there are a couple more we can readily show:
Theorem: An even signal has an even transform:
Proof:
Express ![]() in terms of its real and imaginary parts by
in terms of its real and imaginary parts by
![]() . Note that for a complex signal
. Note that for a complex signal ![]() to be even, both its real and
imaginary parts must be even. Then
to be even, both its real and
imaginary parts must be even. Then
Let even
![\begin{eqnarray*}
X(k)&=&\sum_{n=0}^{N-1}\mbox{even}_n\cdot\mbox{even}_{nk}
+ ...
...10pt]
&=& \mbox{even}_k + j \cdot \mbox{even}_k = \mbox{even}_k.
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img1356.png)
Theorem: A real even signal has a real even transform:
Proof: This follows immediately from setting ![]() in the preceding
proof. From Eq.
in the preceding
proof. From Eq.![]() (7.5), we are left with
(7.5), we are left with
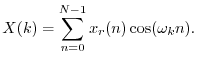
Instead of adapting the previous proof, we can show it directly:
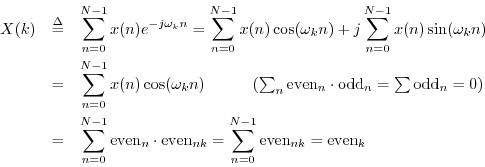
Definition: A signal with a real spectrum (such as any real, even signal)
is often called a zero phase signal. However, note that when
the spectrum goes negative (which it can), the phase is really
![]() , not 0. When a real spectrum is positive at dc (i.e.,
, not 0. When a real spectrum is positive at dc (i.e.,
![]() ), it is then truly zero-phase over at least some band
containing dc (up to the first zero-crossing in frequency). When the
phase switches between 0 and
), it is then truly zero-phase over at least some band
containing dc (up to the first zero-crossing in frequency). When the
phase switches between 0 and ![]() at the zero-crossings of the
(real) spectrum, the spectrum oscillates between being zero phase and
``constant phase''. We can say that all real spectra are
piecewise constant-phase spectra, where the two constant values
are 0 and
at the zero-crossings of the
(real) spectrum, the spectrum oscillates between being zero phase and
``constant phase''. We can say that all real spectra are
piecewise constant-phase spectra, where the two constant values
are 0 and ![]() (or
(or ![]() , which is the same phase as
, which is the same phase as ![]() ). In
practice, such zero-crossings typically occur at low magnitude, such
as in the ``side-lobes'' of the DTFT of a ``zero-centered symmetric
window'' used for spectrum analysis (see Chapter 8 and Book IV
[70]).
). In
practice, such zero-crossings typically occur at low magnitude, such
as in the ``side-lobes'' of the DTFT of a ``zero-centered symmetric
window'' used for spectrum analysis (see Chapter 8 and Book IV
[70]).
Next Section:
Shift Theorem
Previous Section:
Conjugation and Reversal








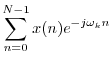
![$\displaystyle \sum_{n=0}^{N-1}[x_r(n)+jx_i(n)] \cos(\omega_k n) - j [x_r(n)+jx_i(n)] \sin(\omega_k n)$](http://www.dsprelated.com/josimages_new/mdft/img1348.png)
![$\displaystyle \sum_{n=0}^{N-1}[x_r(n)\cos(\omega_k n) + x_i(n)\sin(\omega_k n)]$](http://www.dsprelated.com/josimages_new/mdft/img1349.png)











