Figure 7.5:
Illustration of convolution of
![$ y=[1,1,1,1,0,0,0,0]$](http://www.dsprelated.com/josimages_new/mdft/img48.png) and ``matched filter''
and ``matched filter''
![$ h=\protect\hbox{\sc Flip}(y)=[1,0,0,0,0,1,1,1]$](http://www.dsprelated.com/josimages_new/mdft/img1184.png) (
(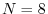 ).
).
![\includegraphics[width=2.5in]{eps/conv}](http://www.dsprelated.com/josimages_new/mdft/img1185.png) |
Figure 7.5 illustrates convolution of
to get
![$\displaystyle y\circledast h = [4,3,2,1,0,1,2,3]. \protect$](http://www.dsprelated.com/josimages_new/mdft/img1187.png) |
(7.3) |
For example,

could be a ``rectangularly windowed
signal, zero-padded by
a factor of 2,'' where the signal happened to be
dc (all

s).
For the
convolution, we need
which is the same as

. When
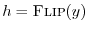
, we say that

is a
matched filter for

.
7.7 In this case,

is matched to look for a
``dc component,'' and also zero-padded by a factor of

. The
zero-padding serves to simulate acyclic convolution using
circular
convolution. Note from Eq.

(
7.3) that the maximum is obtained
in the convolution output at time 0. This peak (the largest
possible if all input signals are limited to
![$ [-1,1]$](http://www.dsprelated.com/josimages_new/mdft/img1190.png)
in magnitude),
indicates the matched filter has ``found'' the dc signal starting at
time 0. This peak would persist in the presence of some amount of
noise and/or
interference from other signals. Thus, matched filtering
is useful for detecting known signals in the presence of
noise and/or
interference [
34].
Next Section: Graphical ConvolutionPrevious Section: Convolution Example 2: ADSR Envelope
![\begin{eqnarray*}
y&=&[1,1,1,1,0,0,0,0] \\
h&=&[1,0,0,0,0,1,1,1]
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img1186.png)
![\begin{eqnarray*}
y&=&[1,1,1,1,0,0,0,0] \\
h&=&[1,0,0,0,0,1,1,1]
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img1186.png)