Free Books
   Free Books    Mathematics of the DFT  

Euler's Identity

Euler's identity (or ``theorem'' or ``formula'') is

$\displaystyle e^{j\theta} = \cos(\theta) + j\sin(\theta) $   (Euler's Identity)

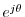
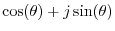
To ``prove'' this, we will first define what we mean by `` $ e^{j\theta }$''. (The right-hand side, $ \cos(\theta) + j\sin(\theta)$, is assumed to be understood.) Since $ e$ is just a particular real number, we only really have to explain what we mean by imaginary exponents. (We'll also see where $ e$ comes from in the process.) Imaginary exponents will be obtained as a generalization of real exponents. 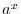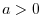Therefore, our first task is to define exactly what we mean by $ a^x$, where $ x$ is any real number, and $ a>0$ is any positive real number.

Next Section:
Positive Integer Exponents
Previous Section:
Complex_Number Problems