Free Books
   Free Books    Mathematics of the DFT  

Positive Integer Exponents

The ``original'' definition of exponents which ``actually makes sense'' applies only to positive integer exponents:

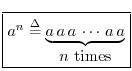
$\displaystyle \zbox {a^n \isdef \underbrace{a\, a \, a \,\cdots \,a \, a}_{\mbox{$n$\ times}}} $

where $ a>0$ is real.

Generalizing this definition involves first noting its abstract mathematical properties, and then making sure these properties are preserved in the generalization.

Next Section:
Properties of Exponents
Previous Section:
Euler's Identity