Exercises
- Show that
where
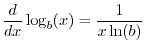
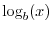denotes the logarithm to the base 
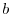of 
.
- Work out the definition of logarithms using a complex base .
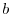- Try synthesizing a sawtooth waveform which increases by 1/2
dB a few times per second, and again using 1/4 dB increments. See if
you agree that quarter-dB increments are ``smooth'' enough for you.
Next Section:
Linear Number Systems
Previous Section:
Voltage, Current, and Resistance
