Free Books
   Free Books    Mathematics of the DFT  

Formal Statement of Taylor's Theorem

Let $ f(x)$ be continuous on a real interval $ I$ containing $ x_0$ (and $ x$), and let $ f^{(n)}(x)$ exist at $ x$ and $ f^{(n+1)}(\xi)$ be continuous for all $ \xi\in I$. Then we have the following Taylor series expansion:

\begin{eqnarray*} f(x) = f(x_0) &+& \frac{1}{1}f^\prime(x_0)(x-x_0) \\ [10pt] &... ...&+& \frac{1}{n!}f^{(n+1)}(x_0)(x-x_0)^n\\ [10pt] &+& R_{n+1}(x) \end{eqnarray*}

where $ R_{n+1}(x)$ is called the remainder term. Then Taylor's theorem [63, pp. 95-96] provides that there exists some $ \xi$ between $ x$ and $ x_0$ such that

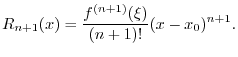
$\displaystyle R_{n+1}(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}. $

In particular, if $ \vert f^{(n+1)}\vert\leq M$ in $ I$, then

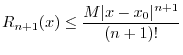
$\displaystyle R_{n+1}(x) \leq \frac{M \vert x-x_0\vert^{n+1}}{(n+1)!} $

which is normally small when $ x$ is close to $ x_0$.

When $ x_0=0$, the Taylor series reduces to what is called a Maclaurin series [56, p. 96].

Next Section:
Weierstrass Approximation Theorem
Previous Section:
Taylor Series with Remainder