Free Books    Mathematics of the DFT  

Generalized Complex Sinusoids

We have defined sinusoids and extended the definition to include complex sinusoids. We now extend one more step by allowing for exponential amplitude envelopes:

$\displaystyle y(t) \isdef {\cal A}e^{st} $

where $ {\cal A}$ and $ s$ are complex, and further defined as

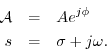
\begin{eqnarray*} {\cal A}&=& Ae^{j\phi} \\ s &=& \sigma + j\omega. \end{eqnarray*}

When $ \sigma=0$, we obtain

$\displaystyle y(t) \isdef {\cal A}e^{j\omega t} = A e^{j\phi} e^{j\omega t} = A e^{j(\omega t + \phi)} $

which is the complex sinusoid at amplitude $ A$, frequency $ \omega$, and phase $ \phi$. More generally, we have

\begin{eqnarray*} y(t) &\isdef & {\cal A}e^{st} \\ &\isdef & A e^{j\phi} e^{(\... ... t} \left[\cos(\omega t + \phi) + j\sin(\omega t + \phi)\right]. \end{eqnarray*}

Defining $ \tau = -1/\sigma$, we see that the generalized complex sinusoid is just the complex sinusoid we had before with an exponential envelope:

\begin{eqnarray*} \mbox{re}\left\{y(t)\right\} &=& A e^{- t/\tau} \cos(\omega t ... ...{im}\left\{y(t)\right\} &=& A e^{- t/\tau} \sin(\omega t + \phi) \end{eqnarray*}

Next Section:
Sampled Sinusoids
Previous Section:
Analytic Signals and Hilbert Transform Filters