Other Lp Norms

Since our main norm is the square root of a sum of squares,

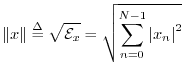
$\displaystyle \Vert x\Vert \isdef \sqrt{{\cal E}_x} = \sqrt{\sum_{n=0}^{N-1}\left\vert x_n\right\vert^2}$ $\displaystyle \mbox{(norm of $x$)}$ $\displaystyle ,$

we are using what is called an norm and we may write $\Vert x\Vert _2$ to emphasize this fact.

We could equally well have chosen a normalized norm:

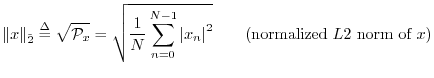
$\displaystyle \Vert x\Vert _{\tilde{2}} \isdef \sqrt{{\cal P}_x} = \sqrt{\frac{... ...N-1} \left\vert x_n\right\vert^2} \qquad \mbox{(normalized $L2$\ norm of $x$)}$

which is simply the ``RMS level'' of

(``Root Mean Square'').

More generally, the (unnormalized) norm of $x\in{\bf C}^N$ is defined as

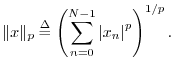
$\displaystyle \Vert x\Vert _p \isdef \left(\sum_{n=0}^{N-1}\left\vert x_n\right\vert^p\right)^{1/p}.$

(The normalized case would include

in front of the summation.) The most interesting

norms are

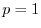: The 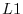, ``absolute value,'' or ``city block'' norm.
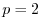: The , ``Euclidean,'' ``root energy,'' or ``least squares'' norm.
$p=\infty$ : The 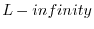, ``Chebyshev,'' ``supremum,'' ``minimax,'' or ``uniform'' norm.