Free Books    Mathematics of the DFT  

Powers of z

Choose any two complex numbers $ z_0$ and $ z_1$, and form the sequence

$\displaystyle x(n) \isdef z_0 z_1^n, \quad n=0,1,2,3,\ldots\,. \protect$ (4.10)

What are the properties of this signal? Writing the complex numbers as

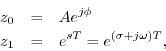
\begin{eqnarray*} z_0 &=& A e^{j\phi} \\ z_1 &=& e^{sT} = e^{(\sigma + j\omega)T}, \end{eqnarray*}

we see that the signal $ x(n)$ is always a discrete-time generalized (exponentially enveloped) complex sinusoid:

$\displaystyle x(n) = A e^{\sigma n T} e^{j(\omega n T + \phi)} $

Figure 4.17 shows a plot of a generalized (exponentially decaying, $ \sigma<0$) complex sinusoid versus time.

Figure 4.17: Exponentially decaying complex sinusoid and projections.
\includegraphics[scale=0.8]{eps/circledecaying}

Note that the left projection (onto the $ z$ plane) is a decaying spiral, the lower projection (real-part vs. time) is an exponentially decaying cosine, and the upper projection (imaginary-part vs. time) is an exponentially enveloped sine wave.

Next Section:
Phasor and Carrier Components of Sinusoids
Previous Section:
Sampled Sinusoids