Phasor and Carrier Components of Sinusoids

If we restrict

in Eq. $\,$ (4.10) to have unit modulus, then $\sigma=0$ and we obtain a discrete-time complex sinusoid.

$\displaystyle x(n) \isdef z_0 z_1^n = \left(Ae^{j\phi}\right) e^{j\omega n T} = A e^{j(\omega n T+\phi)}, \quad n=0,1,2,3,\ldots \protect$

(4.11)

where we have defined

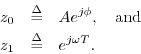
$\begin{eqnarray*} z_0 &\isdef & Ae^{j\phi}, \quad \hbox{and}\\ z_1 &\isdef & e^{j\omega T}. \end{eqnarray*}$

Phasor

It is common terminology to call $z_0 = Ae^{j\phi}$ the complex sinusoid's phasor, and $z_1^n = e^{j\omega n T}$ its carrier wave. For a real sinusoid,

$\displaystyle x_r(n) \isdef A \cos(\omega n T+\phi),$

the phasor is again defined as $z_0 = Ae^{j\phi}$ and the carrier is $z_1^n = e^{j\omega n T}$ . However, in this case, the real sinusoid is recovered from its complex-sinusoid counterpart by taking the real part:

$\displaystyle x_r(n) =$ re $\displaystyle \left\{z_0z_1^n\right\}$

The phasor magnitude $\left\vert z_0\right\vert=A$ is the amplitude of the sinusoid. The phasor angle $\angle{z_0}=\phi$ is the phase of the sinusoid. When working with complex sinusoids, as in Eq. $\,$ (4.11), the phasor representation $Ae^{j\phi}$ of a sinusoid can be thought of as simply the complex amplitude of the sinusoid. I.e., it is the complex constant that multiplies the carrier term $e^{j\omega nT}$ .

Why Phasors are Important

Linear, time-invariant (LTI) systems can be said to perform only four operations on a signal: copying, scaling, delaying, and adding. As a result, each output is always a linear combination of delayed copies of the input signal(s). (A linear combination is simply a weighted sum, as discussed in §5.6.) In any linear combination of delayed copies of a complex sinusoid

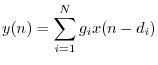
$\displaystyle y(n) = \sum_{i=1}^N g_i x(n-d_i)$

where

is a weighting factor,

is the

th delay, and

$\displaystyle x(n)\isdef e^{j\omega nT}$

is a complex sinusoid, the ``carrier term'' $e^{j\omega nT}$ can be ``factored out'' of the linear combination:

$\begin{eqnarray*} y(n) &=& \sum_{i=1}^N g_i e^{j[\omega (n-d_i)T]} = \sum_{i=1}... ...e^{-j \omega d_i T} = x(n) \sum_{i=1}^N g_i e^{-j \omega d_i T} \end{eqnarray*}$

The operation of the LTI system on a complex sinusoid is thus reduced to a calculation involving only phasors, which are simply complex numbers. Since every signal can be expressed as a linear combination of complex sinusoids, this analysis can be applied to any signal by expanding the signal into its weighted sum of complex sinusoids (i.e., by expressing it as an inverse Fourier transform).

Next Section:
Importance of Generalized Complex Sinusoids
Previous Section:
Powers of z