Free Books    Mathematics of the DFT  

Projection

The orthogonal projection (or simply ``projection'') of $ y\in{\bf C}^N$ onto $ x\in{\bf C}^N$ is defined by

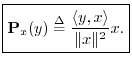
$\displaystyle \zbox {{\bf P}_{x}(y) \isdef \frac{\left<y,x\right>}{\Vert x\Vert^2} x.} $

The complex scalar $ \left<y,x\right>/\Vert x\Vert^2$ is called the coefficient of projection. When projecting $ y$ onto a unit length vector $ x$, the coefficient of projection is simply the inner product of $ y$ with $ x$.

Motivation: The basic idea of orthogonal projection of $ y$ onto $ x$ is to ``drop a perpendicular'' from $ y$ onto $ x$ to define a new vector along $ x$ which we call the ``projection'' of $ y$ onto $ x$. This is illustrated for $ N=2$ in Fig.5.9 for $ x= [4,1]$ and $ y=[2,3]$, in which case

$\displaystyle {\bf P}_{x}(y) \isdef \frac{\left<y,x\right>}{\Vert x\Vert^2} x ... ...{1})}{4^2+1^2} x = \frac{11}{17} x= \left[\frac{44}{17},\frac{11}{17}\right]. $

Figure: Projection of $ y$ onto $ x$ in 2D space.
\includegraphics[scale=0.7]{eps/proj}

Derivation: (1) Since any projection onto $ x$ must lie along the line collinear with $ x$, write the projection as $ {\bf P}_{x}(y)=\alpha x$. (2) Since by definition the projection error $ y-{\bf P}_{x}(y)$ is orthogonal to $ x$, we must have

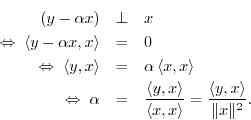
\begin{eqnarray*} (y-\alpha x) & \perp & x\\ \;\Leftrightarrow\;\left<y-\alpha... ...}{\left<x,x\right>} = \frac{\left<y,x\right>}{\Vert x\Vert^2}. \end{eqnarray*}

Thus,

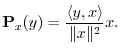
$\displaystyle {\bf P}_{x}(y) = \frac{\left<y,x\right>}{\Vert x\Vert^2} x. $

See §I.3.3 for illustration of orthogonal projection in matlab.

Next Section:
Changing Coordinates
Previous Section:
The Pythagorean Theorem in N-Space