DSPRelated.com
Free Books
   Free Books    Mathematics of the DFT  

Projection

As discussed in §5.9.9, the orthogonal projection of $ y\in{\bf C}^N$ onto $ x\in{\bf C}^N$ is defined by

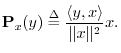
$\displaystyle {\bf P}_{x}(y) \isdef \frac{\left<y,x\right>}{\Vert x\Vert^2} x. $

In matlab, the projection of the length-N column-vector y onto the length-N column-vector x may therefore be computed as follows:
yx = (x' * y) * (x' * x)^(-1) * x
More generally, a length-N column-vector y can be projected onto the $ M$-dimensional subspace spanned by the columns of the N $ \times$ M matrix X:
yX = X * (X' * X)^(-1) * X' * y
Orthogonal projection, like any finite-dimensional linear operator, can be represented by a matrix. In this case, the $ N\times N$ matrix
PX = X * (X' * X)^(-1) * X'
is called the projection matrix.I.2Subspace projection is an example in which the power of matrix linear algebra notation is evident.

Projection Example 1 

>> X = [[1;2;3],[1;0;1]]
X =

   1   1
   2   0
   3   1

>> PX = X * (X' * X)^(-1) * X'
PX =

   0.66667  -0.33333   0.33333
  -0.33333   0.66667   0.33333
   0.33333   0.33333   0.66667

>> y = [2;4;6]
y =

   2
   4
   6

>> yX = PX * y
yX =

   2.0000
   4.0000
   6.0000

Since y in this example already lies in the column-space of X, orthogonal projection onto that space has no effect.

Projection Example 2

Let X and PX be defined as Example 1, but now let

>> y = [1;-1;1]
y =

   1
  -1
   1

>> yX = PX * y
yX =

   1.33333
  -0.66667
   0.66667

>> yX' * (y-yX)
ans = -7.0316e-16

>> eps
ans =  2.2204e-16

In the last step above, we verified that the projection yX is orthogonal to the ``projection error'' y-yX, at least to machine precision. The eps variable holds ``machine epsilon'' which is the numerical distance between $ 1.0$ and the next representable number in double-precision floating point.

Next Section:
Orthogonal Basis Computation
Previous Section:
Vector Cosine