Roots of Unity
Since
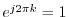 for every integer
for every integer  ,
we
can write
,
we
can write
These are the
 th roots of unity
th roots of unity. The special case
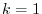
is
called a
primitive  th root of unity
th root of unity,
since integer powers
of it give all of the others:
The

th roots of unity are so frequently used that they are often
given a special notation in the
signal processing literature:
where
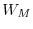
denotes a primitive

th root of
unity.
3.7 We may also call
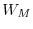
a
generator of the
mathematical
group consisting of the

th roots of unity and
their products.
We will learn later that the  th roots of unity are used to generate
all the sinusoids used by the length-
th roots of unity are used to generate
all the sinusoids used by the length- DFT and its inverse.
The
DFT and its inverse.
The  th complex sinusoid used in a DFT of length
th complex sinusoid used in a DFT of length  is given by
is given by
where
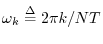
,
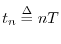
, and
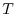
is the
sampling interval in seconds.
Next Section: Direct Proof of De Moivre's TheoremPrevious Section: Back to Mth Roots
![]() for every integer
for every integer ![]() ,
we
can write
,
we
can write
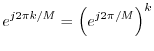
![]() th roots of unity are used to generate
all the sinusoids used by the length-
th roots of unity are used to generate
all the sinusoids used by the length-![]() DFT and its inverse.
The
DFT and its inverse.
The ![]() th complex sinusoid used in a DFT of length
th complex sinusoid used in a DFT of length ![]() is given by
is given by



















