Free Books    Mathematics of the DFT  

Scaling Theorem

The scaling theorem (or similarity theorem) provides that if you horizontally ``stretch'' a signal by the factor $ \alpha$ in the time domain, you ``squeeze'' its Fourier transform by the same factor in the frequency domain. This is an important general Fourier duality relationship.


Theorem: For all continuous-time functions $ x(t)$ possessing a Fourier transform,

$\displaystyle \zbox {\hbox{\sc Scale}_\alpha(x) \;\longleftrightarrow\;\left\vert\alpha\right\vert\hbox{\sc Scale}_{(1/\alpha)}(X)} $

where

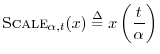
$\displaystyle \hbox{\sc Scale}_{\alpha,t}(x) \isdef x\left(\frac{t}{\alpha}\right) $

and $ \alpha$ is any nonzero real number (the abscissa stretch factor).


Proof: Taking the Fourier transform of the stretched signals gives

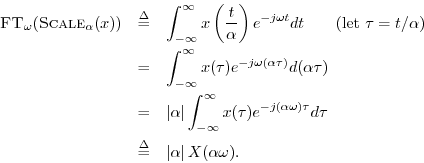
\begin{eqnarray*} \hbox{\sc FT}_{\omega}(\hbox{\sc Scale}_\alpha(x)) &\isdef & ... ...\tau \\ &\isdef & \left\vert\alpha\right\vert X(\alpha\omega). \end{eqnarray*}

The absolute value appears above because, when $ \alpha<0$, $ d (\alpha\tau) < 0$, which brings out a minus sign in front of the integral from $ -\infty$ to $ \infty$.

The scaling theorem is fundamentally restricted to the continuous-time, continuous-frequency (Fourier transform) case. The closest we came to the scaling theorem among the DFT theorems was the stretch theorem (§7.4.10). We found that ``stretching'' a discrete-time signal by the integer factor $ \alpha$ (filling in between samples with zeros) corresponded to the spectrum being repeated $ \alpha$ times around the unit circle. As a result, the ``baseband'' copy of the spectrum ``shrinks'' in width (relative to $ 2\pi $) by the factor $ \alpha$. Similarly, stretching a signal using interpolation (instead of zero-fill) corresponded to the same repeated spectrum with the spectral copies zeroed out. The spectrum of the interpolated signal can therefore be seen as having been stretched by the inverse of the time-domain stretch factor. In summary, the stretch theorem for DFTs can be viewed as the discrete-time, discrete-frequency counterpart of the scaling theorem for Fourier Transforms.

Next Section:
The Uncertainty Principle
Previous Section:
Differentiation Theorem