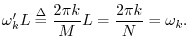Stretch Theorem (Repeat Theorem)
Theorem: For all
![]() ,
,
Proof:
Recall the stretch operator:
![$\displaystyle \hbox{\sc Stretch}_{L,m}(x) \isdef
\left\{\begin{array}{ll}
x(...
...=\mbox{integer} \\ [5pt]
0, & m/L\neq \mbox{integer} \\
\end{array} \right.
$](http://www.dsprelated.com/josimages_new/mdft/img1430.png)

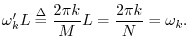
Next Section:
Downsampling Theorem (Aliasing Theorem)
Previous Section:
Rayleigh Energy Theorem (Parseval's Theorem)
Theorem: For all
![]() ,
,
Proof:
Recall the stretch operator:
![$\displaystyle \hbox{\sc Stretch}_{L,m}(x) \isdef
\left\{\begin{array}{ll}
x(...
...=\mbox{integer} \\ [5pt]
0, & m/L\neq \mbox{integer} \\
\end{array} \right.
$](http://www.dsprelated.com/josimages_new/mdft/img1430.png)