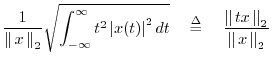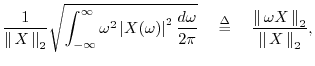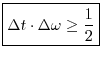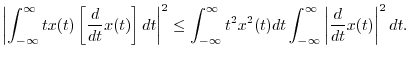The Uncertainty Principle

The uncertainty principle (for Fourier transform pairs) follows immediately from the scaling theorem. It may be loosely stated as

Time Duration $\times$ Frequency Bandwidth $\geq$ c

where

is some constant determined by the precise definitions of ``duration'' in the time domain and ``bandwidth'' in the frequency domain.

If duration and bandwidth are defined as the ``nonzero interval,'' then we obtain $c=\infty$ , which is not very useful. This conclusion follows immediately from the definition of the Fourier transform and its inverse in §B.2.

Duration and Bandwidth as Second Moments

More interesting definitions of duration and bandwidth are obtained for nonzero signals using the normalized second moments of the squared magnitude:

$\displaystyle \Delta t$	$\displaystyle \isdef$	$\displaystyle \frac{1}{\left\Vert\,x\,\right\Vert _2} \sqrt{\int_{-\infty}^\inf... ...sdef \quad \frac{\left\Vert\,tx\,\right\Vert _2}{\left\Vert\,x\,\right\Vert _2}$
$\displaystyle \Delta \omega$	$\displaystyle \isdef$	$\displaystyle \frac{1}{\left\Vert\,X\,\right\Vert _2} \sqrt{\int_{-\infty}^\inf... ...left\Vert\,\omega X\,\right\Vert _2}{\left\Vert\,X\,\right\Vert _2}, \protect$	(C.1)

where

$\begin{eqnarray*} \nonumber \\ [10pt] \left\Vert\,x\,\right\Vert _2^2 &\isdef &... ...}^\infty \left\vert X(\omega)\right\vert^2 \frac{d\omega}{2\pi}. \end{eqnarray*}$

By the DTFT power theorem, which is proved in a manner analogous to the DFT case in §7.4.8, we have $\left\Vert\,x\,\right\Vert _2=\left\Vert\,X\,\right\Vert _2$ . Note that writing `` $\left\Vert\,tx\,\right\Vert _2$ '' and `` $\left\Vert\,\omega X\,\right\Vert _2$ '' is an abuse of notation, but a convenient one. These duration/bandwidth definitions are routinely used in physics, e.g., in connection with the Heisenberg uncertainty principle.^C.1Under these definitions, we have the following theorem [52, p. 273-274]:

Theorem: If $x(t) \ne 0$ and $\sqrt{\vert t\vert}\,x(t) \to 0$ as $\left\vert t\right\vert\to\infty$ , then

$\displaystyle \zbox {\Delta t\cdot \Delta \omega \geq \frac{1}{2}} \protect$

(C.2)

with equality if and only if

$\displaystyle x(t) = Ae^{-\alpha t^2}, \quad \alpha>0, \quad A\ne 0.$

That is, only the Gaussian function (also known as the ``bell curve'' or ``normal curve'') achieves the lower bound on the time-bandwidth product.

Proof: Without loss of generality, we may take consider to be real and normalized to have unit norm ( $\left\Vert\,x\,\right\Vert _2=1$ ). From the Schwarz inequality (see §5.9.3 for the discrete-time case),

$\displaystyle \left\vert\int_{-\infty}^\infty t x(t) \left[\frac{d}{dt}x(t)\rig... ...) dt \int_{-\infty}^\infty \left\vert\frac{d}{dt}x(t)\right\vert^2 dt. \protect$

(C.3)

The left-hand side can be evaluated using integration by parts:

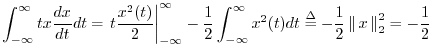
$\displaystyle \int_{-\infty}^\infty tx \frac{dx}{dt} dt = \left . t \frac{x^2(t... ...ty x^2(t) dt \isdef -\frac{1}{2}\left\Vert\,x\,\right\Vert _2^2 = -\frac{1}{2}$

where we used the assumption that $\sqrt{\vert t\vert}\,x(t) \to 0$ as $\left\vert t\right\vert\to\infty$ .

The second term on the right-hand side of Eq. $\,$ (C.3) can be evaluated using the power theorem (§7.4.8 proves the discrete-time case) and differentiation theorem (§C.1 above):

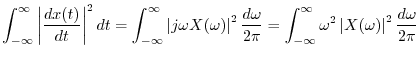
$\displaystyle \int_{-\infty}^\infty \left\vert\frac{dx(t)}{dt}\right\vert^2 dt ... ...\infty}^\infty \omega^2 \left\vert X(\omega)\right\vert^2 \frac{d\omega}{2\pi}$

Substituting these evaluations into Eq. $\,$ (C.3) gives

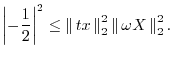
$\displaystyle \left\vert-\frac{1}{2}\right\vert^2 \leq \left\Vert\,tx\,\right\Vert _2^2 \left\Vert\,\omega X\,\right\Vert _2^2.$

Taking the square root of both sides gives the uncertainty relation sought.

If equality holds in the uncertainty relation Eq. $\,$ (C.2), then Eq. $\,$ (C.3) implies

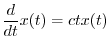
$\displaystyle \frac{d}{dt}x(t) = c t x(t)$

for some constant

, which implies $x(t)=A e^{\frac{c}{2} t^2}$ for some constants

and

. Since $x(\pm\infty)=0$ by hypothesis, we have

while $A\ne 0$ remains arbitrary.

Time-Limited Signals

If for $\left\vert t\right\vert\geq \Delta t/2$ , then

$\displaystyle \Delta t\cdot\Delta \omega \geq \pi$

where $\Delta \omega$ is as defined above in Eq. $\,$ (C.1).

Proof: See [52, pp. 274-5].

Time-Bandwidth Products are Unbounded Above

We have considered two lower bounds for the time-bandwidth product based on two different definitions of duration in time. In the opposite direction, there is no upper bound on time-bandwidth product. To see this, imagine filtering an arbitrary signal with an allpass filter.^C.2 The allpass filter cannot affect bandwidth $\Delta \omega$ , but the duration $\Delta t$ can be arbitrarily extended by successive applications of the allpass filter.

Next Section:
Introduction to Sampling
Previous Section:
Scaling Theorem