Free Books    Mathematics of the DFT  

Spectral Phase

As for the phase of the spectrum, what do we expect? We have chosen the sinusoid phase offset to be zero. The window is causal and symmetric about its middle. Therefore, we expect a linear phase term with slope $ -(M-1)/2=-15$ samples (as discussed in connection with the shift theorem in §7.4.4). Also, the window transform has sidelobes which cause a phase of $ \pi $ radians to switch in and out. Thus, we expect to see samples of a straight line (with slope $ -15$ samples) across the main lobe of the window transform, together with a switching offset by $ \pi $ in every other sidelobe away from the main lobe, starting with the immediately adjacent sidelobes.

In Fig.8.9(a), we can see the negatively sloped line across the main lobe of the window transform, but the sidelobes are hard to follow. Even the unwrapped phase in Fig.8.9(b) is not as clear as it could be. This is because a phase jump of $ \pi $ radians and $ -\pi$ radians are equally valid, as is any odd multiple of $ \pi $ radians. In the case of the unwrapped phase, all phase jumps are by $ +\pi$ starting near frequency $ 0.3$. Figure 8.9(c) shows what could be considered the ``canonical'' unwrapped phase for this example: We see a linear phase segment across the main lobe as before, and outside the main lobe, we have a continuation of that linear phase across all of the positive sidelobes, and only a $ \pi $-radian deviation from that linear phase across the negative sidelobes. In other words, we see a straight linear phase at the desired slope interrupted by temporary jumps of $ \pi $ radians. To obtain unwrapped phase of this type, the unwrap function needs to alternate the sign of successive phase-jumps by $ \pi $ radians; this could be implemented, for example, by detecting jumps-by-$ \pi $ to within some numerical tolerance and using a bit of state to enforce alternation of $ +\pi$ with $ -\pi$.

To convert the expected phase slope from $ -15$ ``radians per (rad/sec)'' to ``radians per cycle-per-sample,'' we need to multiply by ``radians per cycle,'' or $ 2\pi $. Thus, in Fig.8.9(c), we expect a slope of $ -94.2$ radians per unit normalized frequency, or $ -9.42$ radians per $ 0.1$ cycles-per-sample, and this looks about right, judging from the plot.

Figure 8.9: Spectral phase and two different phase unwrappings.
\includegraphics{eps/% specphs-wrapped}
Raw spectral phase and its interpolation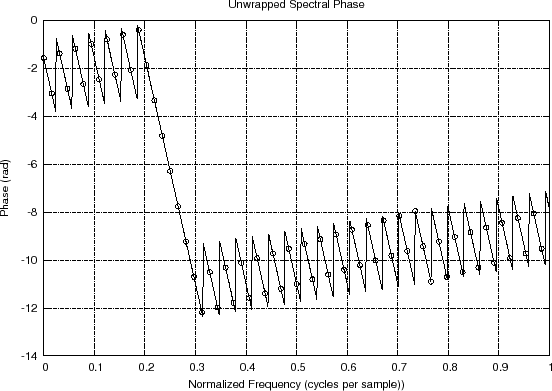

\includegraphics{eps/% specphs-unwrapped}
Unwrapped spectral phase and its interpolation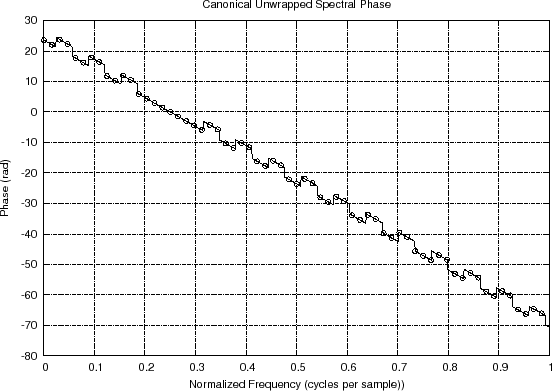

\includegraphics{eps/% specphs-unwrapped-linear}
Canonically unwrapped spectral phase and its interpolation

Next Section:
Radix 2 FFT Complexity is N Log N
Previous Section:
Hann Window Spectrum Analysis Results