Free Books    Mathematics of the DFT  

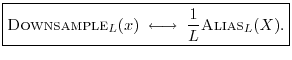
Downsampling Theorem (Aliasing Theorem)


Theorem: For all $ x\in{\bf C}^N$,

$\displaystyle \zbox {\hbox{\sc Downsample}_L(x) \;\longleftrightarrow\;\frac{1}{L}\hbox{\sc Alias}_L(X).} $


Proof: Let $ k^\prime \in[0,M-1]$ denote the frequency index in the aliased spectrum, and let $ Y(k^\prime )\isdef \hbox{\sc Alias}_{L,k^\prime }(X)$. Then $ Y$ is length $ M=N/L$, where $ L$ is the downsampling factor. We have

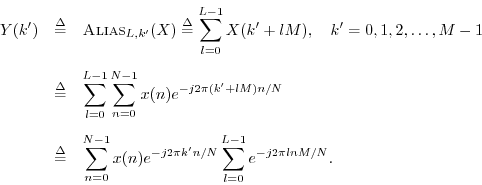
\begin{eqnarray*} Y(k^\prime ) &\isdef & \hbox{\sc Alias}_{L,k^\prime }(X) \isd... ...n) e^{-j2\pi k^\prime n/N} \sum_{l=0}^{L-1}e^{-j2\pi l n M/N}. \end{eqnarray*}

Since $ M/N=1/L$, the sum over $ l$ becomes

$\displaystyle \sum_{l=0}^{L-1}\left[e^{-j2\pi n/L}\right]^l = \frac{1-e^{-j2\p... ...ht) \\ [5pt] 0, & n\neq 0 \left(\mbox{mod}\;L\right) \\ \end{array} \right. $

using the closed form expression for a geometric series derived in §6.1. We see that the sum over $ L$ effectively samples $ x$ every $ L$ samples. This can be expressed in the previous formula by defining $ m\isdeftext n/L$ which ranges only over the nonzero samples:

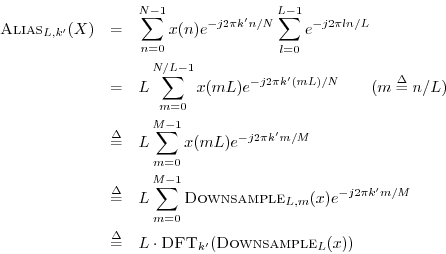
\begin{eqnarray*} \hbox{\sc Alias}_{L,k^\prime }(X) &=& \sum_{n=0}^{N-1}x(n) e^{... ... & L\cdot \hbox{\sc DFT}_{k^\prime }(\hbox{\sc Downsample}_L(x)) \end{eqnarray*}

Since the above derivation also works in reverse, the theorem is proved.

An illustration of aliasing in the frequency domain is shown in Fig.7.12.

Illustration of the Downsampling/Aliasing Theorem in Matlab 

>> N=4;
>> x = 1:N;
>> X = fft(x);
>> x2 = x(1:2:N);
>> fft(x2)                         % FFT(Downsample(x,2))
ans =
    4   -2
>> (X(1:N/2) + X(N/2 + 1:N))/2     % (1/2) Alias(X,2)
ans =
    4   -2

Next Section:
Zero Padding Theorem (Spectral Interpolation)
Previous Section:
Stretch Theorem (Repeat Theorem)