Why Phasors are Important
Linear, time-invariant (LTI) systems can be said to perform only four operations on a signal: copying, scaling, delaying, and adding. As a result, each output is always a linear combination of delayed copies of the input signal(s). (A linear combination is simply a weighted sum, as discussed in §5.6.) In any linear combination of delayed copies of a complex sinusoid
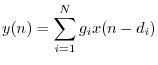
![\begin{eqnarray*}
y(n) &=& \sum_{i=1}^N g_i e^{j[\omega (n-d_i)T]}
= \sum_{i=1}...
...e^{-j \omega d_i T}
= x(n) \sum_{i=1}^N g_i e^{-j \omega d_i T}
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img636.png)
The operation of the LTI system on a complex sinusoid is thus reduced to a calculation involving only phasors, which are simply complex numbers.
Since every signal can be expressed as a linear combination of complex sinusoids, this analysis can be applied to any signal by expanding the signal into its weighted sum of complex sinusoids (i.e., by expressing it as an inverse Fourier transform).
Next Section:
An Example of Changing Coordinates in 2D
Previous Section:
Phasor




















