An Example of Changing Coordinates in 2D
As a simple example, let's pick the following pair of new coordinate vectors in 2D:
![\begin{eqnarray*}
\sv_0 &\isdef & [1,1] \\
\sv_1 &\isdef & [1,-1]
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img905.png)
These happen to be the DFT sinusoids for ![]() having frequencies
having frequencies ![]() (``dc'') and
(``dc'') and ![]() (half the sampling rate). (The sampled complex
sinusoids of the DFT reduce to real numbers only for
(half the sampling rate). (The sampled complex
sinusoids of the DFT reduce to real numbers only for ![]() and
and ![]() .) We
already showed in an earlier example that these vectors are orthogonal. However, they are not orthonormal since the norm is
.) We
already showed in an earlier example that these vectors are orthogonal. However, they are not orthonormal since the norm is
![]() in each case. Let's try projecting
in each case. Let's try projecting ![]() onto these vectors and
seeing if we can reconstruct by summing the projections.
onto these vectors and
seeing if we can reconstruct by summing the projections.
The projection of ![]() onto
onto ![]() is, by
definition,5.12
is, by
definition,5.12
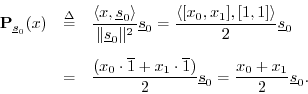
Similarly, the projection of ![]() onto
onto ![]() is
is
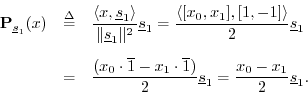
The sum of these projections is then
![\begin{eqnarray*}
{\bf P}_{\sv_0}(x) + {\bf P}_{\sv_1}(x) &=&
\frac{x_0 + x_1}...
...} - \frac{x_0 - x_1}{2}\right) \\ [5pt]
&=& (x_0,x_1) \isdef x.
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img915.png)
It worked!
Next Section:
Examples
Previous Section:
Why Phasors are Important



















