Free Books    Mathematics of the DFT  

Zero Padding Theorem (Spectral Interpolation)

A fundamental tool in practical spectrum analysis is zero padding. This theorem shows that zero padding in the time domain corresponds to ideal interpolation in the frequency domain (for time-limited signals):


Theorem: For any $ x\in{\bf C}^N$

$\displaystyle \zbox {\hbox{\sc ZeroPad}_{LN}(x) \;\longleftrightarrow\;\hbox{\sc Interp}_L(X)} $

where $ \hbox{\sc ZeroPad}()$ was defined in Eq.$ \,$(7.4), followed by the definition of $ \hbox{\sc Interp}()$.


Proof: Let $ M=LN$ with $ L\geq 1$. Then

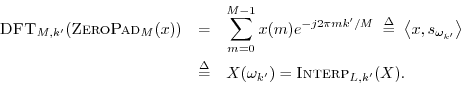
\begin{eqnarray*} \hbox{\sc DFT}_{M,k^\prime }(\hbox{\sc ZeroPad}_M(x)) &=& \su... ...ef & X(\omega_{k^\prime }) = \hbox{\sc Interp}_{L,k^\prime }(X). \end{eqnarray*}

Thus, this theorem follows directly from the definition of the ideal interpolation operator $ \hbox{\sc Interp}()$. See §8.1.3 for an example of zero-padding in spectrum analysis.

Next Section:
Periodic Interpolation (Spectral Zero Padding)
Previous Section:
Downsampling Theorem (Aliasing Theorem)