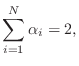Alpha Parameters
It is customary in the wave digital filter literature to define the alpha parameters as
where
We see that
Next Section:
Reflection Coefficient, Parallel Case
Previous Section:
Compatible Port Connections
It is customary in the wave digital filter literature to define the alpha parameters as